機体の性能と打ち上げ能力
この記事のメイントピックです。機体の性能の指標は何か、そしてどのように決まるか説明をします!
打ち上げ能力の指標1.:ΔV (デルタブイ)
ロケットの能力を示す指標はΔV、単位は[km/s]であると説明をしました。単位から分かる通りここでポイントとなるのはΔVの単位は距離でなく、速度になります。宇宙空間では空気抵抗がないため、移動距離そのものでは燃料を消費せず、加減速の時に速度変化分だけ燃料が消費されます。この変化がΔVです。
例えば重力も抵抗も存在しない宇宙空間にいるとしましょう。静止状態から100km/hまで一気に加速して、一時間後にまた静止した場合、移動距離は100kmです。そして合計の加減速、加速と原則それぞれで100km/hつまり合計ΔVは200km/hです。減速が10時間後であれば移動距離は1000kmになりますが、移動距離とは関係なくΔVは変わりません。
ΔVは加減速だけで、移動距離は関係ない。。?でもより遠くへ運ぶ能力のことじゃないの?どういうこと?
先程の例では理想的な条件でしたが、宇宙空間では一定の軌道を描く場合を除き、必ず惑星や太陽の重力を受けます。一切の加減速を行わない場合、この重力によって速度が変わってきてしまい、目標地点まで到達することができません。地表にいる場合はエンジンを止めたら落下しますよね。
宇宙機ではエンジンと点けたり止めたりしながら、最も少ない加減速で目標地点に到達する軌道を探る作業を行います。様々な検討の結果最終的に最適軌道で到達できた場合の必要な合計ΔVがその宇宙機に必要な最低能力ということになります。
軌道を作り込む作業を軌道設計と呼び、人気の最適化問題の一つです。限られた条件下では自動的に最適軌道が導かれることもありますが大体は最後は人力の職人芸です。
打ち上げ能力の指標2.:ペイロード
機体の大きさに対して搭載可能なペイロード(=貨物)の重量を“ペイロードレシオ”と呼びます。仮にΔVが同じ場合、ペイロードレシオが高い機体のほうが性能が良いと言えます。
機体の小型化は射場の設備の簡素化ができたり、消費する推進剤が減らせたり、メリットがたくさんあり、機体開発で最も重きが置かれるところです。
ペイロードとΔVは相関関係にあり、どちらかを犠牲にすることでもう片方を向上させることができます。
重い荷物よりも軽い荷物のほうが遠くまで飛べる飛行機と同じってことだよね。
はい、ということですね。その関係は下記のように表されます。
\[
m_0 = m_f \exp(\frac{\Delta V}{Isp \times g})
\]
\( g: 重力加速度 (9.81の固定値) \)
\( m_f: 燃料を使い切った後の機体+ペイロードの重量 \)
\( m_0: 打ち上げ時、燃料が満タンの時の機体の重量 \)
\( Isp: エンジンの燃費の指標。次章で説明 \)
mfからペイロードの重量を引いたものが機体本体の重量となり、mfとm0の割合を“マスレシオ (Mass Ratio)” や“構造効率” と呼びます。機体の重量に対してどれだけの燃料を搭載できるかの指標になります。
その他の特性
なんだか距離と重さだけって言うけど、乗り心地とかは関係ないのかな、貨物だから?
もちろん、これ以外にも振動が少なかったり、何度もエンジンを繰り返し点火が出来たり、より魅力的なサービスとなりうる機能はあります。しかし、あくまで積載量と運送距離という観点ではロケットの性能はほぼほぼ上記2点、ΔVとペイロードで決まります。
機体が貨物に対してどのような環境であるか (温度や振動、加速度、騒音等の様々な条件)を示したものが、“Payload Users Manual”と呼ばれる取説で、顧客向けに無料で公開されています。これを読めば打ち上げをしたい衛星がどのような環境に耐えられなければならないのかが分かります。

Ariane 5の事例:
https://www.arianespace.com/wp-content/uploads/2015/09/Ariane5_users_manual_Issue5_July2011.pdf
エンジンと機体の性能
ここまで来て、初めて機体に対する具体的な性能要求が決まります。積載能力~kgのトラックにはエンジンの馬力は~必要といった感じですね。
機体が目標とする打ち上げ能力を達成するためには、下記の性能の達成が必要です。これらを機体の要求性能と言います。
- エンジンIsp: エンジンの燃費の指標。つまり単位時間辺りに発生する推力に対して消費する燃料の割合を示します。
- エンジン推力: 損失がない場合は推力が変わっても打ち上げ能力は変わりません。現実には後述する重力損失や制御損失の低減に効きます。
- 機体重量効率: 燃料を除いた機体本体の重さの割合。(m0 – mf)/m0
- 空力効率: 上記に比べると影響は少ないものの空力損失に効きます。ただしほとんどのロケットは細長い円筒形なので空気抵抗よりも安定性に関わります。
打ち上げ能力の計算方法
機体の性能目標が定まったところで、どのように打ち上げ能力を算出するのか見てみましょう。
機体の諸元とパラメータ
ロケットの打ち上げ能力の正確な計算には、具体的な飛行経路を仮定した軌道設計が必要です。3DoF (4DoF)* 解析のために必要な諸元として下記のようなものが挙げられます。
- エンジン推力: 大気圧によって変わるため、逐次計算が必要です
- エンジンIsp: 大気圧によって変わるため、逐次計算が必要です
- 機体空虚重量: 燃料がない状態の機体の重量(=mf – ペイロード)
- 機体全備重量: 燃料を満タンにして打ち上げ状態にした重量 (=m0)
- 空力損失係数: 迎え角に対する抗力・揚力傾斜
- 大気密度情報:各高度の大気密度。天気予報が超重要です。
- 横風履歴:各高度の横風の情報。天気予報が超重要です。
- ペイロード重量
- 投棄物重量:フェアリングの重さと捨てるタイミングです。
上記の諸元を用いて軌道設計を行って行きますが、これは最適化問題の一種です。どのような飛行経路を辿るかは計算をしてみないと分からず、下記のパラメータを変えながら計算します。
- 機体の向き(姿勢角):各時刻におけるロケットの向きです。エンジンを動かすことで向きたい方向に舵取りをします。
- 推力の大きさ: 推力調性が可能な機体であれば、絞りを入れることも可能です
なんだか設計で決まってしまうパラメータに対して制御できるパラメータって結構少ないんだね、、、
まさにそう!ロケットの打ち上げが難しい理由は、言ってしまえば“ほとんど制御不能”だからです。
例えるならばアクセルほぼ全開のままハンドル操作だけで目的地に定刻通りに到着しなければ行けない状態です。そうなると車体自体の性能が良くないと運転できたものではなく、ぶつかってしまいますよね。
より単純な問題として、推力を発生せず、地球が平らだと仮定した場合の弾丸のケースを過去記事で紹介しているので、興味のある方は是非こちらも読んでみてくださいね。(*3DoF、6DoFや自由度についてもこちらに書いています! )
諸元の重要性について
ロケットは機体の後ろにエンジンがついており翼を持たないため、エンジンを左右に動かすジンバリング動作によって機体の向きを制御しています。これは倒立振子問題と呼ばれる状態で常に不安定なため、エンジンの向きを微調整し続けないと機体が引っくり返ってしまいます。ジンバルの動きはこんな感じです。
エンジンを動かしてバランスを保つのは手のひらの上にバットを置いてバランスを保つために手を動かすのと同じイメージだよね。
ジンバリングによって得られる横向きの力は機体を傾ける力となり“制御力”と呼びます。機体の推力や重量、重心位置、空力荷重などから決まる“空力荷重と制御力のバランス”が成り立っている条件では横風などの外乱があってもエンジンを向きを変えれば調整可能です。しかし制御力を上回る外乱が加わった場合は、機体は制御を失ってしまいます。制御工学の専門分野でよく言われる“系の安定限界”に該当するものです。
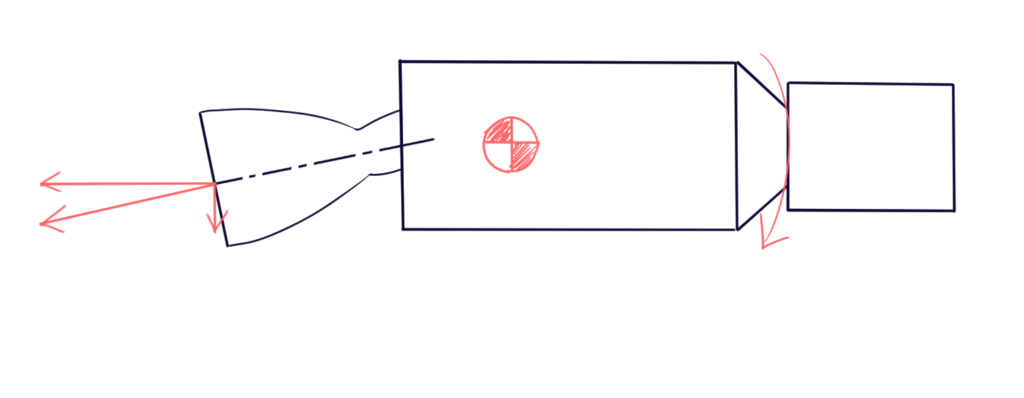
エンジンを動かして機体の向きを変える動き
打ち上げの実況とかで出てくるmaxQっていう用語はこれのこと、、、?
それは少し違ってて、maxQは空力荷重が一番大きくなる点。つまり機体の構造が一番厳しい点です。しかし本当に制御で厳しくなるのはその後で、燃料が少なくなると機体が軽くなるためわずかな外乱でもすぐに引っくり返ってしまいます。諸元によってタイミングは異なりますが、ほとんどの場合はmaxQの後です。
大気圏を抜けてしまえば外乱はほとんどなくなるため一安心です。(その次には分離とSEIGというドキドキがありますが)
諸元が決まった段階でロケットの安定性は理論的な限界が決まってしまいます。そのため、大本の諸元がダメだと”制御プログラムでなんとか~”という誤魔化しが効かないのです。後から諸元を変えるのは至難の業のため初期の段階で十分な検討が必要で、ロケット開発がなかなかアジャイル化ができない理由の一つです。
エンジン一基が止まってしまい推力=制御力が不足してしまったロケットは目標軌道まで到達できないばかりか、最悪下の動画のようになってしまいます。制御力が空力モーメントに負けてしまっている状態です。
軌道設計について
地球の重力や大気は一定だし、そもそも最適な軌道って射場が決まったら大体同じなんじゃないの?
残念ながら機体毎に異なります。軌道に到達するためには地表に対して水平に加速し、第一宇宙速度まで到達する必要がありますが、そこに至るまでは下記のようなパターンが考えられます。
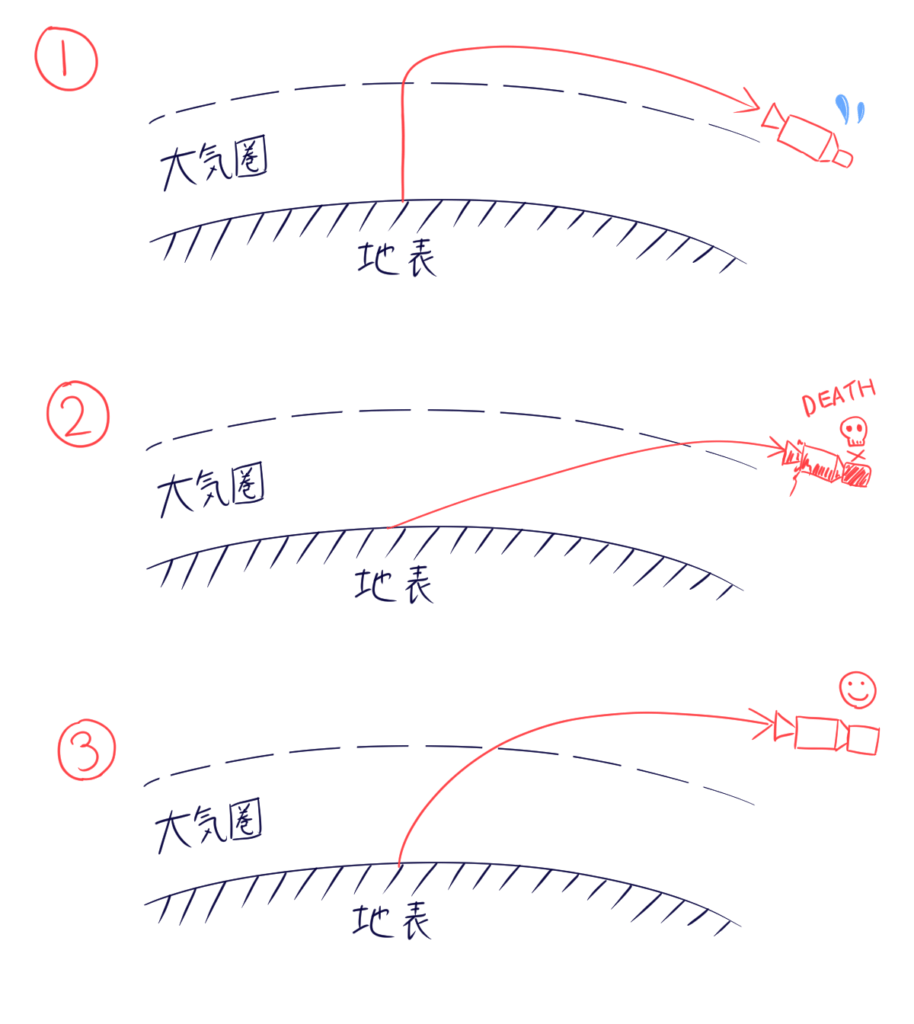
- 空気抵抗を最小化する場合:空気抵抗のみを減らすことを考えると、図1のように地面から垂直に打ち上げをして、大気圏を抜けたところで90°回転して横に加速する方法です。しかしこの場合垂直に上昇している間は常に重力がかかり続けるため、例えば推力が機体の1.5倍あっても0.5gでしか加速できず推力の2/3は無駄になってしまいます。これを“重力損失”と呼びます。そしてそもそもロケットはマッハ5で飛行中にいきなり90°進路を変えることはできません。
- 重力損失を最小化する場合:それでは次にいきなり真横に加速した場合はどうでしょうか。重力損失は最小化できますが、大気圏を抜けるのに時間がかかり、今度は空力損失が大きくなってしまいます。さらには、これを実際にやろうとすると地面に激突してしまうので空想上の話だということが分かります。無理やりロケットのパワーでやったとしても大気圏再突入と同じような状態なので機体は燃え尽きてしまいます。
- 現実の最適軌道:上記の理由で現実的な軌道としては①と②の中間のような、垂直に上がって滑らかに横向きになるようなものです。最適な軌道はロケットの推力や空力性能以外にも当日の風や大気密度の影響も受けてしまうことが分かるかと思います。
機体が自然と重力で倒れる速度と軌道を垂直から横向きに遷移させたい速度にぴったりと合わせてあげるとエンジンのジンバリングが不要になり、“重力ターン”や“ゼロリフトターン”という方法が実現できます。
多かれ少なかれこの原理を応用して最小限のロスを目指した機体はあるものの、日本のL-4Sは唯一重力ターンのみを用いて無誘導で打ち上げられた成功例です。
細かい話
これまで多くのパラメータが登場しましたが、実はこれだけでは軌道を正確に計算することはできません。更に本格的な6DoF解析を行うためには下記の要因も考えることが必要です。
ええ、、まだあるの。。。??
機体のおおよその能力を測る上では、これまでのパラメータだけでも十分だし、それ以上の諸元はメーカーでないとまず手に入れることはできません。ただしいざ機体を作って飛ばすとなるほ他にも考えるべきことがいくつかあります。重要なものを挙げると:
- ロール損失:本来機体はロール方向へ動かす必要はありませんが、外乱によって回ってしまうため、これを抑えるのに必要な推力の損失です。
- 慣性モーメント:機体の慣性モーメントで制御設計に必要です。
- 固有モード:機体の曲げと縦方向の固有値及び固有モード形状です。制御設計に必須の他、エンジン振動と機体の錬成を防止するためにも重要です。
- 性能ばらつき:エンジンや機体の個体間のばらつき。性能が良い個体もあれば悪いものもあるので、それぞれの水準での打ち上げ能力の評価が必要です。
- 分離解析:1段目と2段目が分離する時にどのような挙動をするか、エンジンを点火するまでにどれぐらいの間が必要かを計算します。
- 迎角制限:迎え角の制限のこと、ジンバルを動かすことができる範囲と機体の強度で決まります。ロケットは機体が大きくミサイルのようにいきなり曲がったりはできませんが、どこまでならいける、というパラメータが制御設計に必要になります。
- システム応答性、制御遅れ:コンピュータが目標としたい姿勢角を算出しても、信号を処理してからアクチュエータを動かして実際にエンジンが動くまでには時間差があります。この時間遅れを制御モデルに織り込む必要があります。機体の運動自体にもこの遅れが現れるため計算で加味する必要があります。
- 制御損失:制御アルゴリズムに由来するものと、制御遅れによる物理的なものがありますが、制御に起因する損失をΔVに換算したものです。
- 空力加熱:大気との摩擦で耐熱温度に問題が生じないか。固体ロケットのように大推力の機体の場合、前章の②に近い軌道になるため、断熱材などで保護が必要な部位が生じます。当然重量や空力への影響が生じます。
- 保安要件:実は最も重要な条件です。人口密集地域など飛行経路を制限するようなものがないか。ロケットが墜落した場合の安全距離が確保できるかと言った安全面での検討です。
このような検討は機体の性能を推定するだけならばいりませんが、本格的に開発や運用を行っていく上では欠かせません。
たしかに言われてみれば応答遅れとかはある程度設計してみないと分からないよね、、、
潤沢な予算があれば、すべてが分かっていなくてもプロトタイプを作って試しちゃう (某テキサスの会社のように) こともできるのですが、予算が限られているとすべて机上検討で決めてからプロジェクトを開始せざるを得ないのでめちゃくちゃ大変です。。。
計算方法
計算方法は各時刻において、前章で挙げたパラメータを計算します。そして逐次計算によって最終的な獲得ΔVを求めることができます。具体例は簡素化したパラメータを元に次回紹介して行きます。
一度宇宙空間に到達してしまえば、パラメータがかなり減るので計算は楽になり、多くの紹介ページが存在します。
人工衛星の軌道計算人工衛星の打上げシミュレーションプログラム(JavaScript版)
宇宙空間に至るまでが外乱が多くてなかなか難しく、ノウハウベースのパラメータが多数存在します。機体の仕様と軌道の設計は同時に行わなければうまく行かないことが分かって頂けたのではないでしょうか?
おまけ:打ち上げ中の計算
従来の打ち上げでは事前に計算された飛行経路を元に制御パラメータを設計し、計算結果から逸脱した場合は飛行中断としていました。しかし近年は制御落下や自立飛行安全の実装するにあたって、打ち上げを行いながらリアルタイムで計算が行われるようになっています。求められる精度と計算スピードは高まり続けているのです。
次回予告
数多くのパラメータが登場しましたが、簡単に概算するためにはいくつかのパラメータは無視して計算せざるを得ません。次回は第2回、公開情報を用いて簡易的な3DoF解析によりStarshipの打ち上げ能力を推定して行きたいと思います。
本日も読んで頂きありがとうございました!
今回は先に基本的なことを説明したいという思いやボリューム的な理由で1.5回という形で分けてみました。第2回を楽しみにしていた方、、、次回こそはStarship書きたいと思います!お楽しみにしていてください!
また次回お会いしましょう
参考・クレジット
機体に必要な検討と計算のために使える管理人的おすすめ本✩
https://note.com/ina111/n/nbffc9f7d452a
https://gisgeography.com/polar-orbit-sun-synchronous-orbit/
https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB:Orbital_ATK_logo.svg
https://www.mss.co.jp/technology/report/pdf/22-01.pdf

















[…] 【SpaceX】特集 :ロケットの性能についてロケットの性能や打上能力は具体的にどういう指標なのか、どのように決まるのか、について解説します。… […]
[…] 【SpaceX】特集 :ロケットの性能についてロケットの性能や打上能力は具体的にどういう指標なのか、どのように決まるのか、について解説します。… […]