はじめに
さあ、いよいよ本編の始まりだ!本日は風洞試験の評価方法だ。
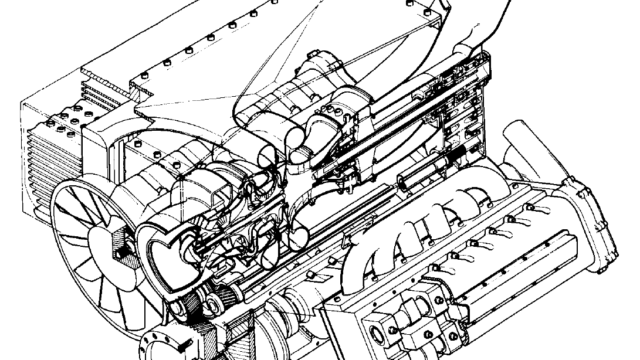
少し昔の文献ですが、風洞試験の結果を整理する時に使われている公式だそうです。。。!
今回は文献を参考に風洞試験結果の評価方法と、各パラメータの感度が測定対象の空力性能評価に与える影響度を見て行きましょう。
前編の記事がまだの方はこちらからどうぞ!
- 前編の続きを読みたい
- 風洞で得られた測定結果の評価方法について知りたい
- 今回の記事のレーティング:
引用文献:
https://www.sae.org/publications/technical-papers/content/2005-01-1457/
車体の空力についての過去記事もあるので、そもそも風洞で何を評価しているのか?を知りたい方はこちらも読んでみてくださいね。
風洞間の相関
前回説明をしたおさらいです。風洞というのは巨大な計測装置の一種ですが、異なる物を測定しても同じ結果が得られる定規などと異なり”同じものを測定しても、風洞によって測定結果がずれる” という困った特性があります。
どうしてずれるか。。?前回を読んでいればなんとなくイメージはできると思うが、実際のところは完全には解明されてはいないんだ。
このため、一般的には同じ風洞で測定を繰り返したり、異なる風洞間では校正球などを用いて結果の補正を行ったりするのだ。
校正球とは、理論流れが把握しやすい球体を風洞の中に入れ、期待される力に対してどれだけのズレがあるか測定することで、風洞の素性を把握する方法です。文字通り、ツルッとした球体なので、流体の教科書通りの特性が得られる(はず)です。
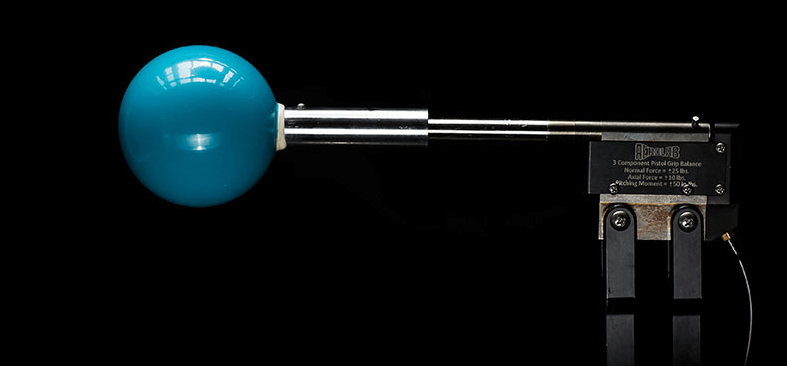
測定結果が乱れる理由
風洞において測定結果がずれる、ということは動圧か静圧のいずれかが変化して、測定物にかかる力が変化するということです。
風洞の形状が違うことによって、流線が変化してしまっているのですね。
そういうこと!具体的にひとつずつ見ていこう。
変動速度の動圧補正
簡易風洞で可視化されたカルマン渦を見てみましょう。果たしてこの時円筒に作用する抗力は一定なのでしょうか?
当然ながら、渦の発生/消滅の周期に応じて力の大きさが変化するよね。
一般的に表現される”Cd値”や”Cl値”は、瞬間瞬間で見ると常に変動しています。そのため、一定時間の定常平均値を用いることが一般的です。変動幅は物体によって異なりますが、ヨー角がついた状態やそもそも流線型でなくウェーキが大きなものでは、平均抗力の数割に達することもあります。
ウェーキが一定周期で発生している場合は、抗力増加側と減少側での差分は均一な正弦波となるため、単純に平均値を用いることで測定が可能です。ただしサンプリング周波数はウェーキの周波数よりも細かいことが前提となります。
風洞での非定常の測定はこのように平均値を前提としているため、困難が伴うことがあります。下図はロードセル生値がどれぐらい大きく変動するか表した一例です。
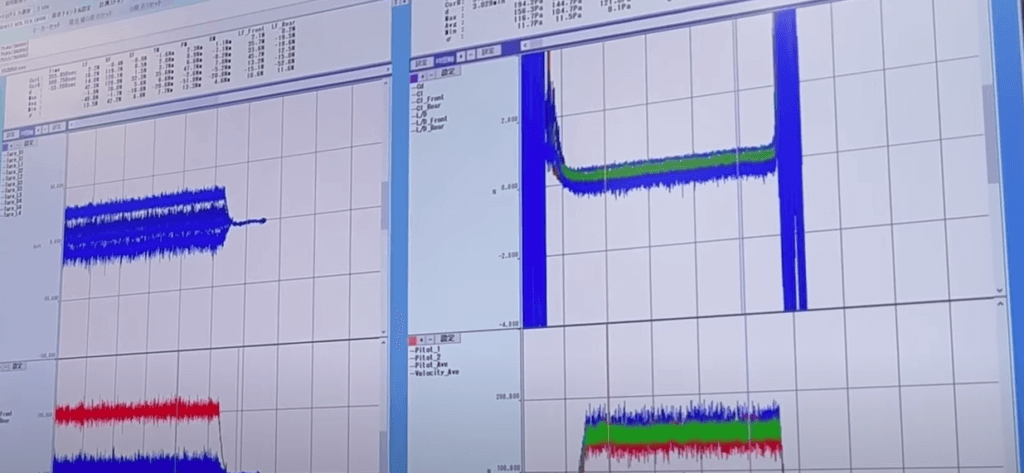
引用元(宣伝です)
乱流の流速分布を測定するのは非常に難しいので、簡易的な方法としては後流での騒音を測定して、各周波数のピークと強度を確認することもできます。下記リンクにwavファイルからFFT変換とプロットができるツールをおいてあるので、気になる方は是非。スマホからでも使えます
https://colab.research.google.com/drive/19o7tcvXi9l2F-iFdlW96cBVlMfszp05E
ブロッケージファクタとクローズド型
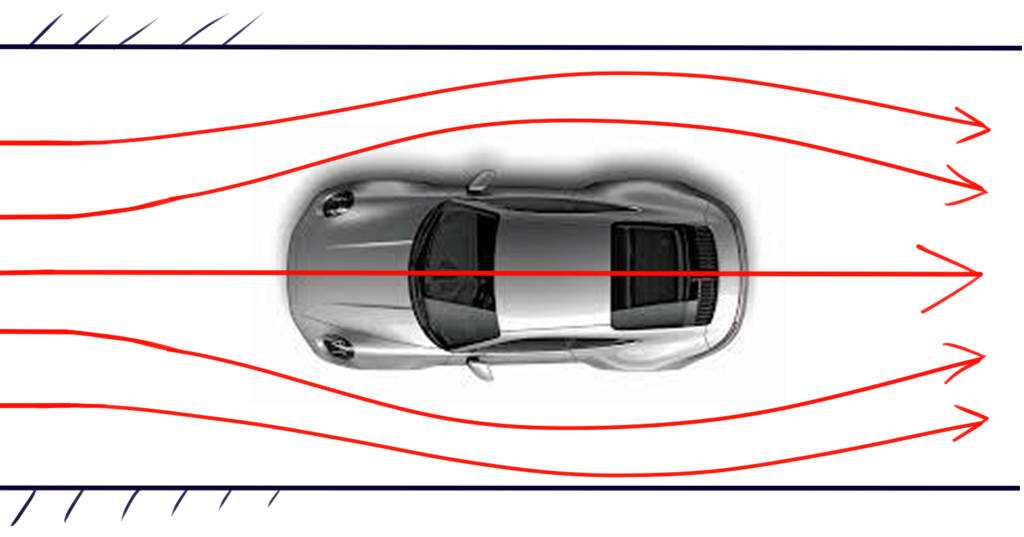
クローズド型風洞では、よっぽど大きな流路面積がない限り、模型によって流路が塞がれてしまいます。下の2つの図を見てみると、”塞がれ具合によって流線が変化する”ということがわかります。この塞がれ具合を示した指標がブロッケージファクタで、投影面積の比率で示されます。
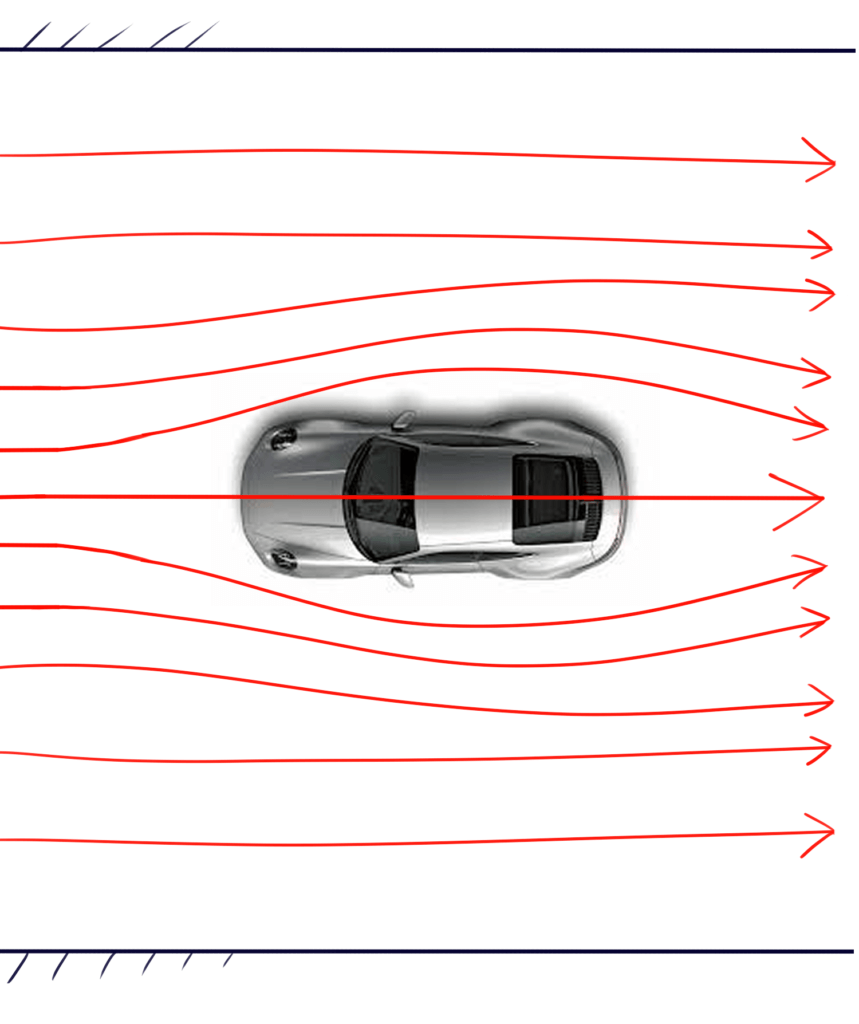
オープン型風洞では、テストセクションは開放されているため、ノズルとコレクタそれぞれに対して、ブロッケージファクタを設定します。
一番直感的な影響だ、補正式は次章で出てくるぞ!
航空機でよく用いられるクローズド型でブロッケージファクタが大きな場合、相応の補正が必要となります。しかし試験によっては実機とのズレが多少出ても十分な場合も多く、その一例が”設計変更前後の差を見る”というような用途です。
例えばこの動画のように737のウィングレットの効果を見るためには、ベースラインとなる機体の性能がわかっていれば十分と言えます。
ノズル・コレクタでの拡大偏向
本質的にはブロッケージと関連しているものの、流線自体がどれぐらい曲げられている、を表した指標です。下図のように、ノズルからテストセクション、コレクタにかけてストレートだった流れが拡散し、再び縮流するため模型に対しては角度がついた状態となり、その影響を補正します。
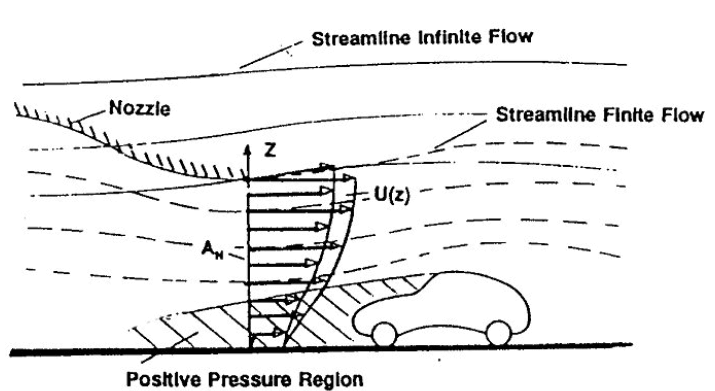
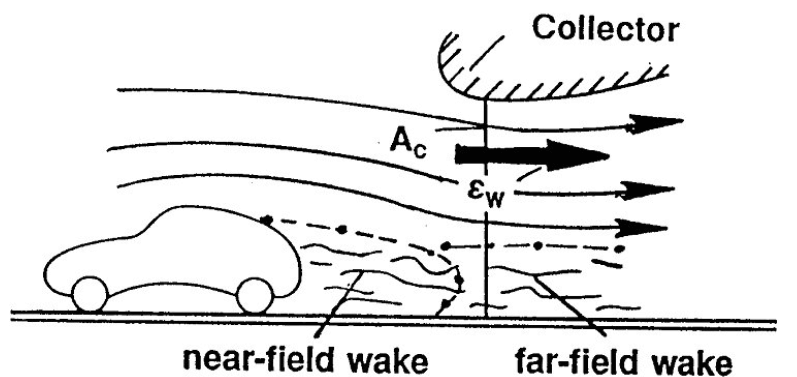
浮力影響
模型の前後左右に静圧差が変化することによって、浮力が発生する現象です。具体的にはノズルとコレクタで発生する圧力勾配によって、模型前後の静圧が変化することで発生します。
壁面境界層
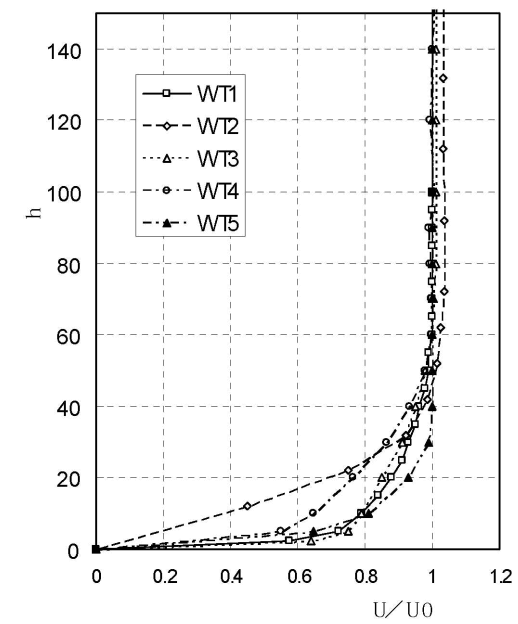
テストセクション壁面の境界層領域では当然ながら流速が下がってしまい、測定ができません。風洞で試験をするもので、ほとんどの場合この影響は問題となりません。しかしその例外となるのが”自動車”と”鉄道”です。地面への距離が近い物体の場合、床面の境界層の処理が必要になります。
こればかりは排除するのが難しい。だから自動車用風洞では条件を揃えるために境界層制御装置 (BLC) が使われ、高価になってしまいがちなんだ。
厄介なのは、この境界層制御のための各種装置の特性が風洞によって異なり、それによって測定結果に差が出てしまう点です。これだけを研究対象とする人も少なくないニッチな分野です。
その他の影響
その他、測定物によって特有の考慮すべき点があります。例えば航空機の場合は主翼のフラッタ、翼端のフラッタ、エンジン排気のウェーキ等です。
自動車の場合は、タイヤの回転影響の他、測定方法によってはサスペンションの影響が出てきてしまいます。
サスペンションただ上下に動くだけでなく、ストロークに応じてトー(左右)やキャンバー(傾き)が変化するように設計されています、つまり横から力を加えると前後のちから(抗力)が発生するこということです。しかも市販車の場合は位置決め剛性が低く、車体に力を加えることで各タイヤが好き勝手な方向に動いてしまうのです。
このような点から自動車の風洞測定は”外乱が大きく””流線型でなく””風洞屋が一番測定したくないもの”のうちのひとつと言えるかもしれません。ある意味風洞の中でも特殊な分野です。
天秤で車体本体を吊らず、四輪を設置させて測定する場合、この影響によって横力が大きく影響を受け、その結果抗力も変化してしまいます。
欧州車は高速域での安定性に優れる=空力に優れると思われがちですが、実はCd値はそれほど変わりません。大きく違うのはCl値とリフトや横力が作用した際の車体の動き=サスペンション特性です。
測定結果の補正方法
それでは先程紹介した各影響の具体的な補正式を見てみよう。
オープンセクションの補正法
E.Merkerのオープンセクションにおける補正式を見てみましょう。
補正抵抗係数:
\( C_{Dcor}=(D_{Dm} + \Delta C_{DHB})/(q_{cor}/q_{\infty}) \)
\( (q_{cor}/q_{\infty}) = (1+\epsilon_S+\epsilon_N+\epsilon_c)^2 \)
ただし
\( C_{Dm} \):計測された抵抗係数
\( \Delta C_{DHB} \) : 水平浮力係数
\( (q_{cor}/q_{\infty}) \):補正/計測動圧
\( \epsilon_S \) 吹出し風拡大・偏向補正
\( \epsilon_N \)ノズルブロッケージ補正
\( \epsilon_c \) コレクタブロッケージ補正
拡大偏向補正
吹出し風拡大・偏向補正
\( \epsilon_S = \tau{(V_m/L_m)^{1/2}}{A_m/(A*)^{3/2}} \)
\( A* = A_N/(1+\epsilon_Q) \)
\( \epsilon_Q = (A_M/2A_N)(1-x_s/(x_s^2+R_N^2)^{1/2}) \)
\( R_N = (2A_N/\pi)^{1/2} \)
\( x_s = x_M – L_M/2 + (A_M/2 \pi)^{1/2} \)
\( \tau = \frac{-0.032}{(1-M^2)^{3/2}}(\frac{2H}{W} + {W/2H})^{0.252} \)
ただし
\( \tau \): 風洞形態係数
\( A_M \): モデル前面面積
\( V_M \): モデル体積
\( L_M \):車両長さ
\( A* \)::偏向補正ノズル断面積
\( R_N \)::ノズル等価半径
\( A_N \): ノズル断面積
\( \epsilon_Q \):ノズル出口変動速度
\( r_N \): ノズル等価半径
\( x_M \): ノズルからモデル中心までの長さ
\( x_s \):ノズルから湧き出し点までの長さ
\( W \): テストセクション幅
\( H \):テストセクション高さ
\( M \):マッハ数
ノズル及びコレクタブロッケージ
ノズル、コレクタブロッケージ補正
\( \epsilon_N = \epsilon_Q R_N^3 / (x_M^2 + R_N^2)^{3/2} \)
\( \epsilon_C = (\epsilon_w R_C^3)/((L_{TS} – x_M)^2 + R_c^2)^{3/2} \)
\( \epsilon_w = (A_M/A_C)(C_{Dm}/4+0.41) \)
\( R_c = (2A_c/\pi)^{1/2} \)
ただし
\( R_c \): コレクタ等価半径
\( \epsilon_W \): 車両ウェイク変動速度
\( L_{TS} \): テストセクション長さ
\( A_c \):コレクタ断面積
浮力
浮力による抗力補正
\( \Delta C_{DHB} = (1.75/A_m)(V_M/2)*G \)
\( G = ((dc_p/dx)_n + (dc_p/dx)_c ) \)
\( (dc_p/dx) \): 局所圧力勾配
添字n, c はそれぞれノズル、コレクタ
クローズドセクションの補正法
次にクローズドセクションでの補正法を見てみましょう。クローズドセクションではオープンセクション同様の浮力補正に加え、ウェイクブロッケージの補正が追加されます。
補正抵抗係数:
\( C_{Dcor}=(C_{Dm} + +\Delta C_{Dw} + \Delta C_{DHB} )/\frac{q_{cor}}{q_{\infty}} \)
\( \frac{q_{cor}}{q_{\infty}} = (1+K_3 \tau’ \frac{2A_{M \Psi} 2 V_M}{\sqrt{L_p 2V_M} (2 A_N)^{3/2}} + \frac{A_M}{A_N} (\frac{1}{4} C_{Dm} + \eta \frac{A_{M \Psi}}{A_M})^2 \)
\( K_3 = 1.0 \)
\( \tau’=0.406 (2H/W + W/2H) \)
\( \eta = 0.41 \)
\( L_p = L_M cos \Psi + W_M sin \Psi \)
\( C_{Dw} = \frac{1}{4} * C_{Dm}^2 A_M / A_N \)
\( C_{Dw} \): ウェイクブロッケージによる補正抵抗係数
\( W \):測定部幅
\( H \): 測定部高さ
\( \Psi \): 偏揺角
\( A_{M \Psi} \): 偏揺れ角時のモデル正面投影面積
物理的になんとなくそうだなというものもあればほぼ経験式のものもあるので、こういう式が使用されている、という理解で良いかなと思います。