前回のあらすじ
前回はB-29の射撃管制装置(FCS)の先進性や、FCSの概要について解説をしましたが、今回はいよいよFCSの動作原理、FCSが偏差を求める際に実際に行っている計算の内容について解説をしていきたいと思います。
射撃管制装置とは?B-29はどこが先進的だったのか? について書かれた前回の記事はこちらからどうぞ!
- FCSの計算内容の仕組みを知りたい
- 人間の感覚とFCSとではどれほどの精度の違いがあるか知りたい
- 今回の記事のマニアック度:
(前半):B-29に搭載された先進的な射撃管制装置を紹介します。
(後半):砲弾の弾道計算とFCSの原理について実例を交えて説明します。
主な内容としては、計算に必要な各種パラメータについて説明をしたのちに、NATO標準規格である、STANAG 4355 MPMTMの4DoFモデルを元に簡素化した計算を行って行きます。
STANAG 4355: MPMTMとは
MPMTM (Modified Point Mass and Trajectory Model)とはNATO諸国が定めた標準化規格:STANAG 4355の通称で、 砲弾や弾道弾の6自由度剛体運動を戦場でもリアルタイム弾道計算に用いることができるように、4ないし5自由度に省略する方法を示したものです。
実際に用いられているのはSG2 S4 という標準化射撃管制ライブラリに組み込まれる標準ロジックになります。ソフトウェアコード本体は軍事機密ではあるものの、ロジックの中身は普通の物理法則をまとめただけのもので、一般の人でもアクセスができるようになっています。
このような標準導入によって、友軍同士で同じ射撃計算結果を共有することができ、共同作戦の立案や兵器の互換性維持をすることができます。古い規格ですが現在でも多くの火砲に使われており、砲術の世界においては非常に重要な計算規格となっています。
要約すると”砲弾をどうやって狙えば良いか、仲間同士で計算方法を決めてしまいましょう。”というものだな!砲科に行くと履修することになるぞ。
砲弾の運動方程式
MPMTMでは一部経験則と省略が用いられるため、まずは砲弾の運動に影響を与えるそれぞれの要素と弾道計算の方法を物理の観点から見てきましょう。
MPMTMをのまま適用すると専門用語も多いため、まず物理の教科書に則って一つひとつの力を分かりやすく解説していこうと思う。
砲弾に作用する力
座標変換について
照準器から見ている”座標”は目標の絶対座標 (x,y,z)ではなく、”どっち方向に距離どれぐらい”といった測定が可能なパラメータから構成されます。このような座標系は球面極座標系(r、θ、φ) で表します。どちらでも弾道の計算はできますが、FCSの特性上絶対座標で計算したほうが楽なため、一度変換を行う必要があります。
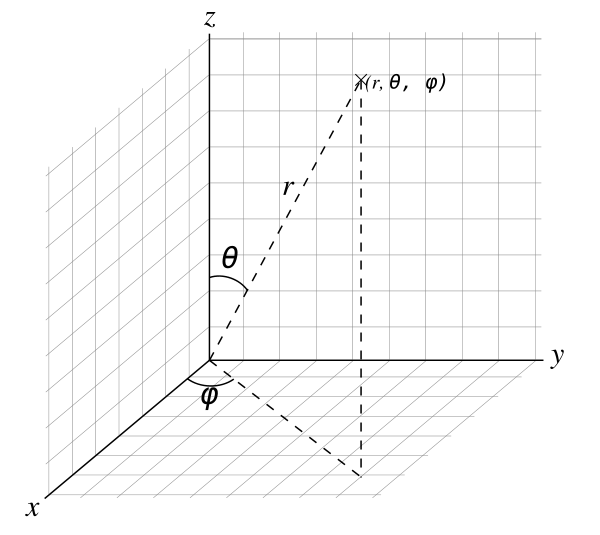
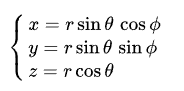
絶対座標との変換は様々な座標変換の方法が教科書やネットに大量に掲載されているため、ここでは変換の詳細は省略をします。
座標変換が分からなくても本日の演習には支障はありません。なぜならば、、、MPMTMでは絶対座標を基準とした規格のため、直行座標系さえ分かれば問題なく計算ができるからなのです!(基本的には解釈の余地なしのため、ここはユーザーに任せています) なので忘れてしまっていても諦めずに読み進めてください。
ちんぷんかんぷんだという人は、ホコリを被った数学IIIの教科書を開いてみよう。きっとこういうのがあったのを思い出すはずだ。でもやり方は思い出さなくても大丈夫。
MPMTMでは発射地点を基準とした、地面に対して直角な直交座標系で計算を行います。また基本的には自信が静止した状態を想定しているものの、運動していても問題なく適用することはできます。
相対ベクトル (位置・速度)
“相対ベクトル”とは直交座標系上での目標との相対位置と相対速度のことです。この差のことを偏差と呼び、偏差を考慮した射撃を偏差射撃と言います。具体的には、シューティングゲームで移動する敵に対して、”見越し射撃”を行ったりしたことがある方も多いかと思います。一般的には偏差射撃というと、この見越しだけのことを指すことも多いです。
ここでは、X,Y,Z軸それぞれを先程の空間の図のように表し、砲弾の最初の位置(時間t=0とした時の位置)は原点として考えます。
\(
\boldsymbol {X_1}: 砲弾の位置 \)
\(
\boldsymbol {X_2}: 目標の位置 \)
\(
\boldsymbol {\Delta X}: 相対位置
\)
\(
\boldsymbol {u}: 砲弾の速度ベクトル \)
\(
\boldsymbol {w}: 風速 \)
\(
\boldsymbol {v}: 風に対する速度ベクトル \)
\(
\)
また加速度は下記のように記述します。
\(
\boldsymbol {\dot{u}}: 砲弾の加速度ベクトル \)
\(
\boldsymbol {u}: 砲弾の速度ベクトル
\)
\( \boldsymbol {X_1 (t=0)} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} , \boldsymbol {\Delta X (t=0)} = \boldsymbol {X_2 (t=0)} \)
同様に、風に対する相対速度は下記の通りになります。
\( \boldsymbol {v} = \boldsymbol {u} – \boldsymbol {w} = \begin{pmatrix} u1 \\ u2 \\ u3 \end{pmatrix} – \begin{pmatrix} w1 \\ w2 \\ w3 \end{pmatrix} \)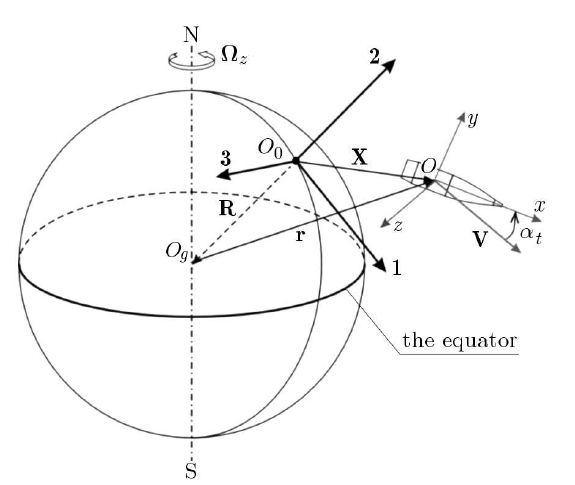
歳差運動 (タンブリング)
現代の弾丸は特殊なものを除けばライフリングによって10万rpm以上で回転しているため、回転するコマのような動きをします。このような運動を章動(振れ)(Synchronous Motion)と、歳差運動(タンブリング)(Precession)と呼び、砲弾の迎角と運動自体に影響を与えます。コマの頭が一定の周期で円運動をするのと同じ動きであることからすみそり運動と呼ばれることもあります。
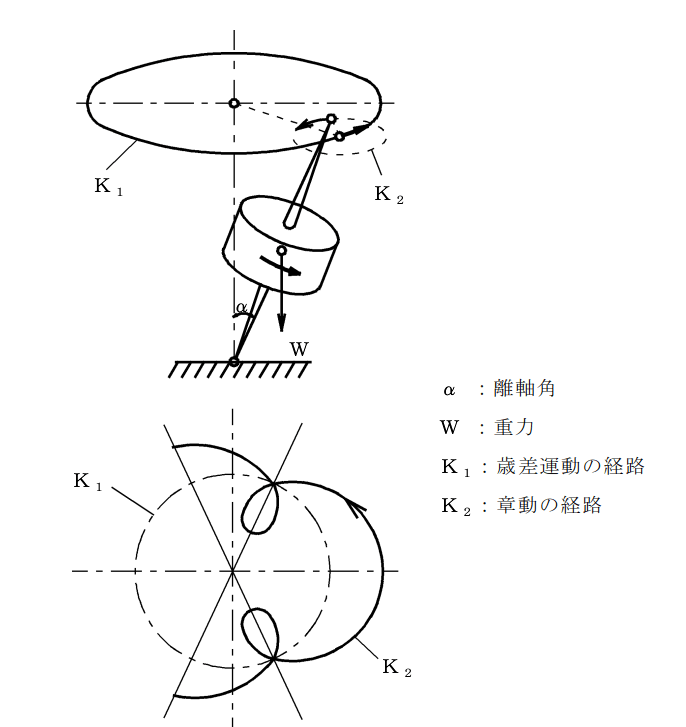
砲弾の回転数に連動した速い章動運動は重心と軸芯のズレで発生し、下図K2のような細かい自転運動となります。これに対して、回転数よりも遅いK1の大きな公転運動が歳差運動です。
毎分10万〜100万回転という超高速回転する弾丸を、厳密に計算をすると、どれほど計算量が大きくなってしまうか、なんとなくイメージできたかな?このような問題があるため、一般的には砲弾の運動では簡略化して考えることが多いんだ。
弾丸に回転を与えるために砲身に加工された溝のことをライフリング、この方式を採用する銃火砲のことをライフルと呼びます。ライフリングの巻数によって弾丸の回転数を制御していて、1インチ当たりの巻数:1/in の単位が用いられることが多いです。

章動運動、歳差運動は回転体とは切っても切り離せない重要な事象で、特にモーターやガスタービンなどの高速で回転する機械では性能に大きな影響を及ぼします。しかし砲弾の場合は章動運動は非常に小さく無視ができることに加え、歳差運動は後述するジャイロ効果によって周期的な回転運動を平均化して考えることができるため、刻一刻とすべての運動を計算しなくても進路予測が可能になります。この省略化の作業がMPMTMのミソになります。
タンブリング・ジャイロ効果
回転をする砲弾にはジャイロ効果が働き、外力に対して軌道を安定化する方向に力が働きます。このように回転を利用して軌道を安定化させる方法はスピン安定と呼ばれ、大多数の弾丸で用いられています。外力とジャイロ効果の釣り合いによって周期的な歳差運動が発生しますが、ジャイロ効果による振れ運動に対して回転体の回転数が十分に早い場合は、同じ公転軌道を描き続けるため瞬間的な触れを考慮する必要はなく、時間平均でのドリフト量のみを考えれば軌道が計算できます。
歳差運動のおおよその周期は下記から得られます:
\( M:重心周りの合計モーメント力 \)
\( I_y: 重心周りのピッチ・ヨー断面二次モーメント \)
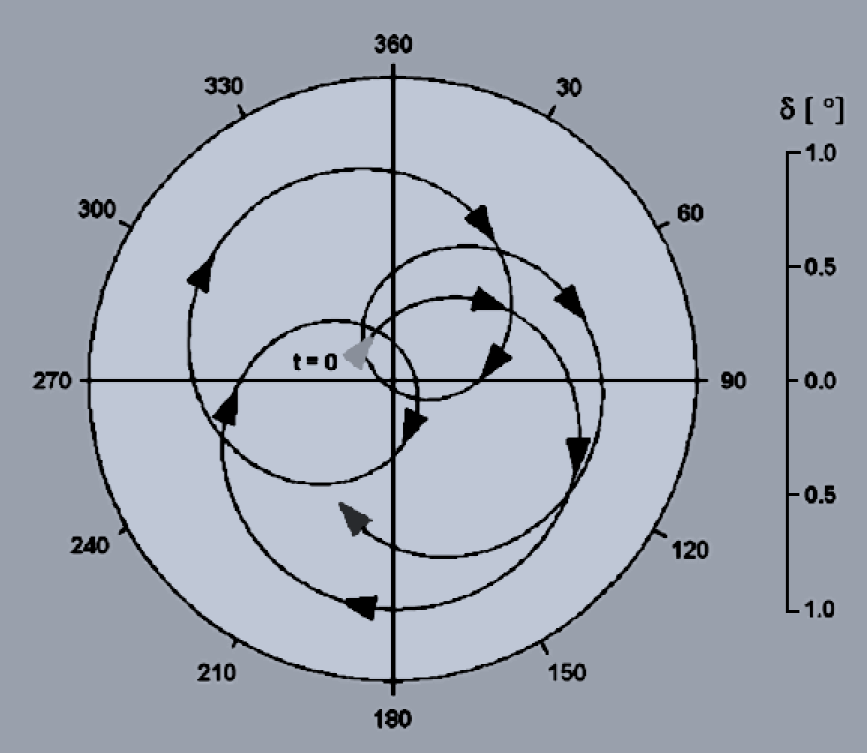
例え安定した軌道であっても、瞬間的な弾丸の動きを線で表すと、このような複雑な軌道を描き、これを時々刻々と計算するためには非常に大きな計算リソースが必要になってしまいます。
ジャイロ効果が外力に対して十分かどうかは、回転数に依存します。安定した軌道を描くためには下記の安定条件を満たす必要があり、これ以下に回転数が落ちてしまうと、空力的に不安定な砲弾はランダム運動へと移行してしまい、進路予測ができなくなってしまいます。
現存する弾丸では回転数の減衰が起きる前に空気抵抗により射程距離が先のため、実は最も安定性が厳しい条件は発射直後なんだ。発射時の安定性が大丈夫なら、基本的には最後まで安定していると考えていい。ライフル弾ではSgは1.5~5.0以下程度とするのが一般的で、高すぎると今度はまた別の問題が起きることもある。
\( s_g > 1\)
弾丸のタンブリングの動きはアメフトのボールをイメージするとわかりやすいです。少しブレながらも安定した軌道を描いて狙ってところに飛んでいくボールと弾丸は非常に似た動きをします。
離軸角・スピンドリフト
歳差運動を平均化した迎角ベクトルをYaw of Repose (離角度)と呼び、進行方向に対して砲弾の向きが平均してどれほどずれているか(離軸角)を表します。迎角によって最終的に砲弾がずれる量をスピンドリフトと呼び、仮に無風であってもこの効果によって砲弾の着地点はずれることがわかっています。
Yaw of Repose (離角度・迎角ベクトル) \(\boldsymbol{\alpha_e} = \begin{pmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_2 \end{pmatrix} \\ \)また、実際の迎角αtとの関係は:
\( \boldsymbol{\alpha_e} = \boldsymbol{i_v} \times (\boldsymbol{x} \times \boldsymbol{i_v}) \)\( \left| \boldsymbol{\alpha_e} \right| = sin(\alpha_t) \)
\( ただしα_t<<1の時は \)
\( \left| \boldsymbol{\alpha_e} \right| = \alpha_t \)
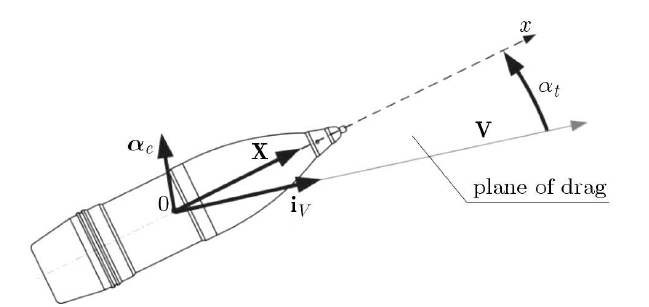
離角度は様々な要因によって決まり外力がないと発生しない力です。そのため、砲身を離れる瞬間はゼロになります。各時刻における外力で決まる値のため、他の力について説明をしたのちに、最後に振り返りたいと思います。
なんやらややこしく感じるかもしれないが、本来は複雑な歳差運動をする砲弾をあたかも真っ直ぐ飛ぶかのように表した時、どのような迎角がついて、どの方向にずれて飛んで行くかを示したのがYaw of reposeと考えて良い。周期的な運動からの変換は数学上の操作が必要なので、ここでは割愛したい。興味がある人は是非関連文献を読んでみてほしい。
この簡素化こそがMPMTMの中核をなす部分で、計算を大幅に簡素化できるんだ。
重力
砲弾が重力の影響で落下する力です。基本的には真下に働きますが、地表から離れるに連れて少し変化します。
\(
m: 砲弾の質量 \)
\(
R: 地球の半径 6.3781 *10^6 [m] \)
\(
\boldsymbol {F_g}: 重力ベクトル \)
\(
g_0 : 重力加速度 =9.80665 [m/s^2]
\)
砲弾に作用する重力は下記の通りになります。
\( \boldsymbol {F_g}= -mg_0 \begin{pmatrix} X_1 R \\ 1 – 2X_2/R \\ X_3 R \end{pmatrix} \)揚力・抗力
砲弾には必ず迎え角度がついているため、揚力や抗力が発生します。それぞれ風向きと揚力係数、抗力係数によって決まり、下記のように表すことができます。
\(
A: 面積係数 = \frac{\pi d^2 }{8}, ただし \)
\(
d = 砲弾の直径 [m^2] \)
\(
\rho = 空気密度 [kg/m^3] \)
\(
C_{D0}:迎え角0の時の抗力係数 \)
\(
C_{D \alpha_2}: 迎え角αの時の抗力係数 \)
\(
Q_D: 砲弾固有の比例係数 \)
\(
C_{L \alpha} 迎角0度の時の揚力係数 \)
\(
C_{L \alpha_3} : 迎角αの時の揚力係数 \)
\(
\boldsymbol{\alpha_e}: Yaw\, of\, Repose\, (離角度) \)
\(
v = \left| \boldsymbol {v} \right| = \sqrt{(v_1^2+v_2^2+v_3^2)}: 砲弾の速度 \)
\(
f_l, i: それぞれ揚力と抗力に関する係数 \)
抗力は迎角の2乗に比例し、下記のように表されます。
\( \boldsymbol {DF} = – \rho A i C_{D}(\alpha) v \cdot{\boldsymbol{v}} \\ \)揚力は下記のように表されます。
\( \boldsymbol {LF} = – \rho A f_l C_{L}(\alpha) v^2 \cdot{\boldsymbol{\alpha_e}} \\ \)また、弾丸の運動方向だけでなく、回転自体の減衰も存在します。回転表面に作用するストークス力による摩擦損失があるためです。しかし他の力に比べると極めて小さく無視することができます。ほとんどの砲弾では着弾時には初期の90%以上の回転数を保っているのが一般的です。
\( \frac{d\omega}{dt} = \frac{\pi \mu d^3 \omega}{I_x} \)ここまでは一般的な運動方程式です。基本的には空気抵抗を考慮したボールを投げた時と同じ動きをします。弾丸自体の回転はほぼ一定の場合がほとんどのため、今回は省略したいと思います。
コリオリ力
コリオリ力とは、飛翔する物体を地上から見た時に進路がそれるように見える、みかけ上の力です。地球の時点によって発生するため、実際に曲がっているわけではありません。例えば飛行機で南北に向かう時に緯度だけでなく経度もズレるため、東西にも向かって飛ぶ必要がありますが、同様の効果が砲弾にも作用します。
\( u: 物体の移動速度 [m/s] \)
\(
\omega_E:地球の時点速度 [rad/s] \)
\(
\theta: 地球上の緯度 [deg] \)
\(
ただし\boldsymbol{u’} は地軸北向きに合わせた絶対座標系 \)
\(
\)
ここで発生するコリオリ力の大きさと、ベクトルは:
\( \left| F_{cor} \right| = 2mu \omega_E sin\theta \)\( \boldsymbol {F_{cor}} = 2 m \omega_E \begin{pmatrix} 0 & sin\theta & -cos\theta \\ -sin\theta & 0 & 0 \\ 0 & cos\theta & 0 \end{pmatrix} \begin{pmatrix} u_1′ \\ u_2′ \\ u_3′ \end{pmatrix} \)
\( \boldsymbol {F_{cor}} = 2m(\boldsymbol{\omega_E} \times \boldsymbol{u}) \)
θ=0では上式はゼロになるので、赤道上ではコリオリ力は発生しないことになります。例えば非常に重量が重い砲弾(抗力や揚力の影響が少ない砲弾)の場合を見てみましょう。赤道上で発射した場合に比べて、北極点で発射した場合は、10km先に向けて射撃する場合7m以上も位置がずれます。
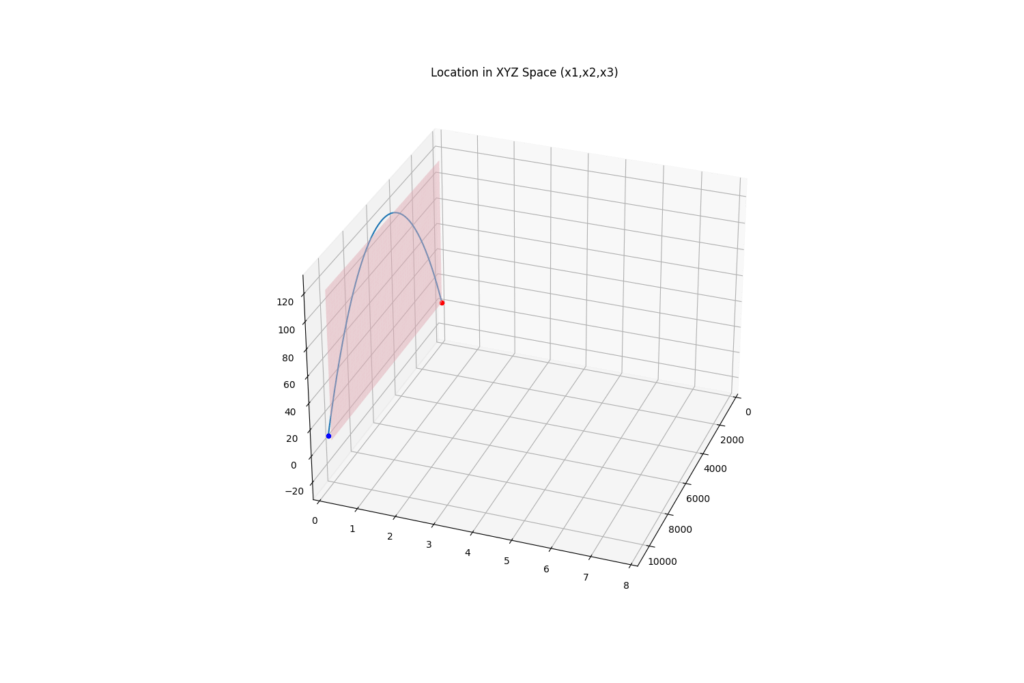
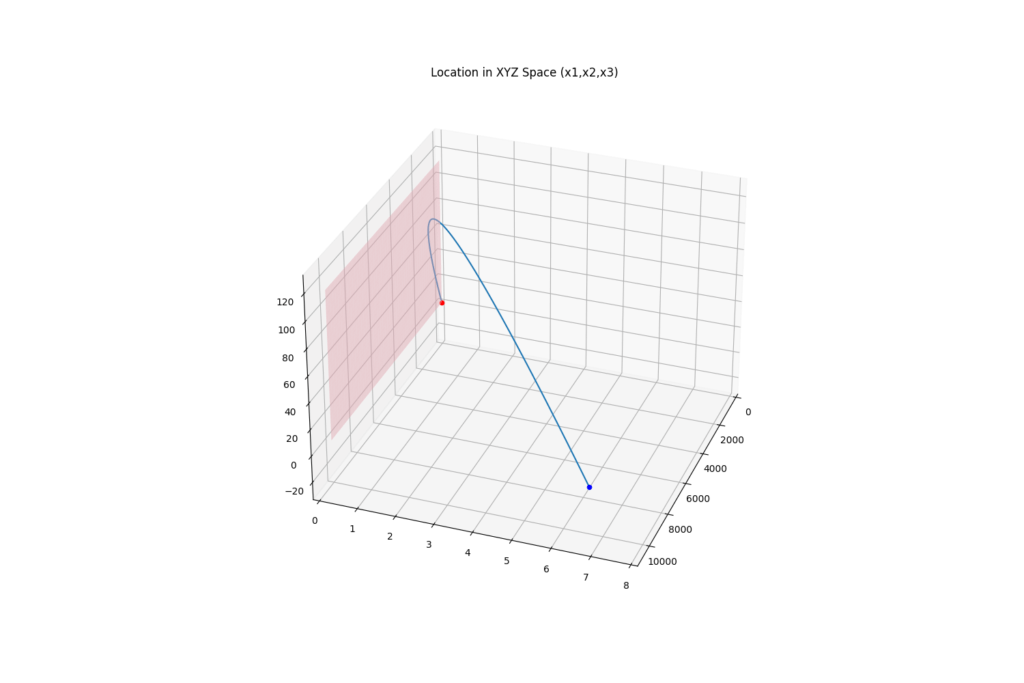
遠距離射撃では無視できない力である一方、赤道付近や極めて近距離ではほとんど影響がでないため、主に地上火砲で重要となります。
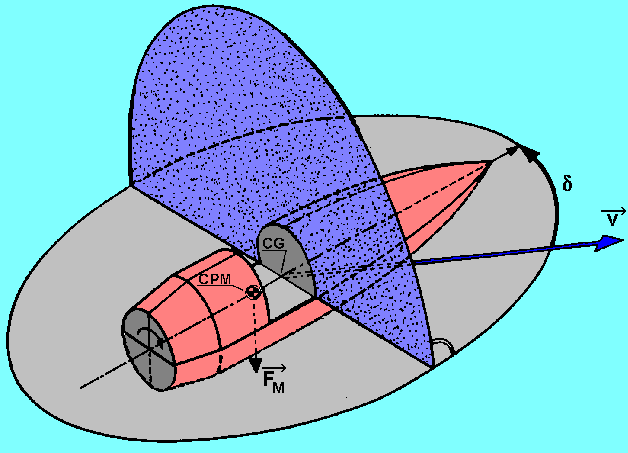
マグヌス効果
マグヌス効果は回転する物体が発生させる力です。カーブやフォークボールを想像するとわかりやすいかと思います。弾丸も高速回転をしているため、横風を受けた場合ボールのように上昇したり下降します。しかも常に迎角は0ではないため、一般的には浮き上がりのような動きをします。
\(
\boldsymbol{MF}: マグヌス力 \)
\(
\rho: 空気密度 \)
\(
Q_M: 係数 \)
\(
\omega: 回転速度 \)
\(
C_{mag}: 揚力係数 \)
\(
\alpha_e: Yaw \ of \ Repose \)
\(
\boldsymbol{v}: 速度ベクトル
\)
球技で経験がある方も多いとは思いますが、距離が伸びればマグヌス効果の影響は非常に大きくなり、下の動画のような”ボールが空を飛んでいる”というような現象にまでなることもあります。
マグヌス効果を利用すると、回転方向を変えることで変化球やスライダーと言ったいろんな球種を投げることができる。ムービーではバックスピンをかけることで球が浮き上がるような力を働かせているんだ。
離軸角 Yaw of Reposeの計算
最後に上記の計算に必要なYaw of Repose αeを求めるには、下記を用います。加速度と対気速度の外積、断面二次モーメント、モーメント外力の釣り合いによってαeが決まることが分かります。先述の通り、αeは迎角をベクトル表記したものなので、各時系列において、時々刻々と変化する迎角が存在します。
\( \boldsymbol{\alpha_e} = \frac{8 I_x \times \omega}{\pi \rho d^3 C_M v^4} \boldsymbol{v} \times \boldsymbol{\frac{du}{dt}} \)ばらつき
仮に計算精度が完璧だったとしても、距離や対気速度の情報等に誤差があると、計算結果にもその誤差が反映されてしまいます。この誤差の蓄積をばらつきと呼び、いかに高精度な大砲であっても命中率が必ず100%とはならない理由です。
ばらつきを推測する方法はいくつかありますが、ベーシックなものとして下記のものがよく用いられます。
- 上下限法(Linear Approximation):上限下限という制限値を設け、その間でいくつかの水準での全体の感度解析を行う方法です。各因子の保証値が決まっている場合に、全体のワーストケースとして考えられる最も極端な結果を得ることができます。
- 二乗平均(Mean Squared):各因子のばらつきの上限下限に対して二乗平均を全体ばらつきとして考える方法。すべての因子が正規分布に従う場合、数%以内の精度で正規分布法と一致するため、多くの規格で用いられています。
- 正規分布法/ボックス=ミュラー法 (Normal Distribution):確率分布が正規分布に則ると仮定して、中央値からの偏差を設定する方法。ボックスミュラー法は簡易的に正規分布を模擬する方法です。少数のサンプル数から正規分布的傾向が認められる場合、用いることが多いです。
- モンテカルロ法 (Monte-Carlo Method):誤差因子それぞれの発生確率から、無作為にばらつきの組み合わせを生成して、全体の期待値を総当り的に求める方法。それぞれの因子がおおよその正規分布に則る場合は、ボックスミュラー法との誤差は数%に収まる場合がほとんどです。最も計算リソースを要する他、各因子の確率モデルを入れてあげる必要があります。
運動方程式
4自由度系
砲弾の運動を先述した歳差運動の省略によって4自由度化を行うことができました。これにより単純にベクトル和が弾丸に作用する力になり、迎角が第四のパラメータとして扱うことができます。厳密にはαeには3成分があり、6変数になりますが、3変数は従属してvとuから決まり独立したものではありません。また瞬間瞬間で見た時には、砲弾がどの向きを向いているかはMPMTMでは計算ができないのです。4自由度と呼ばれる所以はこのためです。
力の釣り合い
力の釣り合いは前項で挙げたすべての力のベクトル和になります。すなわち、F=maより、加速度=(抗力+揚力+マグヌス力+重力+コリオリ力)/重量 です。
\( \dot{u} = (\boldsymbol{DF} + \boldsymbol{LF} + \boldsymbol{MF} + \boldsymbol{F_g} + \boldsymbol{F_{cor}} )/m \)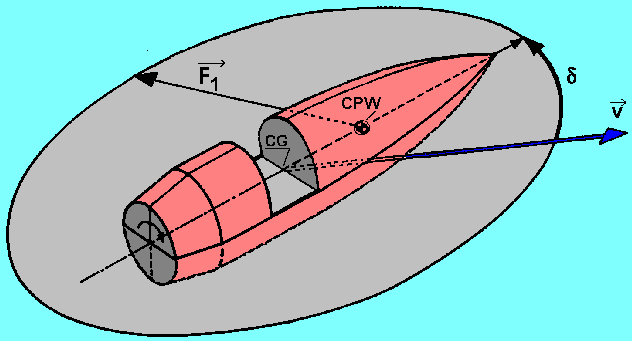
モーメントの釣り合い
モーメントCMはすべての作用力の圧力中心と力の大きさから求まりますが、詳細な値はマッハ数や迎角によって変化するため正確に求めるのが最も難しい力です。さらに、瞬間瞬間で見ると、弾丸は歳差運動をしているため、モーメントの釣り合いは存在せず、常に受ける力に対して直角方向にジャイロ効果が働き、いずれかの方位に対してモーメントが作用している状況です。
モーメントに寄与するのは重心から離れたところに作用する力です、すなわち。
- 抗力:重心よりも前方Cpに作用し、弾丸を不安定化させる方向に働く
- 揚力:抗力と同等
- マグヌス力:マグヌスモーメント中心点に働き、重心よりも後方で弾丸を安定化させる方向に働く
安定条件 Sg > 1.0を満たしてさせいれば、CMの値が大きくても弾丸は安定軌道を描くことができ、平均化した迎角はYaw of Reposeで表すことができます。
少し分かりにくく感じるかもしれないが、瞬間単位でみると、モーメントは釣り合っていないため、ジャイロ力とモーメントの合力によって歳差運動が発生するんだ。
しかし平均化した単位でみると、ほぼほぼYaw of Reposeと同じ迎角のずれが得られるので、このズレによって発生するモーメントとの釣り合いが保たれている状態になるんだ。
解法
上記で示した運動方程式を時間積分をすると時間tの目標の未来位置から、砲弾の初期速度(射撃を行う方向)を求めることができます。また運動方程式は、条件付きで解析解を得ることも可能です。最も簡単な例は等速直線運動をし、外力が作用しない、中学の教科書で出てくるような問題です。
勉強が好きな人は方程式の一般解を導くのも面白いかもしれないな。
しかし解析解が得られない問題はどうしましょう。我々は数学者ではありません。難しいことは考えずに答えだけが知りたいだけなので、力技で解いてしまいましょう。
時間積分はせずに下記の流れで計算していきます。
- 微小時間Δtの間は作用する力は一定と仮定する
- Δtの間の速度、位置の変化を計算する
- 砲弾が目標に命中、あるいは外れるまで逐次計算をする
- 命中しなければ、射撃角度を変更して1.から再計算する。
1.~3.は連続関数を離散化し、線形近似する手法はルンゲ=クッタ法と呼ばれ、多くの数値計算で行われる基本的な手法です。
なお、管理人はややこしい数学は一切分かりません。書いてある数式を脳死でコードに打ち込むだけです!
揚力傾斜やその他比例係数はSTANAG中には記述されておらず、適当にαに比例するようなモデルを仮定して試してみてください。
今回の計算では下記のように仮定し、揚力傾斜は線形として簡素化しました。
#Lift Coefficient
def CLcalc(AOA):
if AOA > 10:
CL=0.01
elif AOA < -10:
CL=0.01
else:
CL=0.04*AOA/10 + 0.04
return(CL)
#Drag coefficient
def CDcalc(AOA):
CD=0.4*AOA/10 + 0.4
return(CD)
#Overturning moment
def CMcalc(AOA):
CM=0.05*AOA/10 + 0.05
return(CM)
c_fl=1.05 #Coefficient f for lift range fitting factor
c_i=1.02 #Coefficient i for lift range fitting factor
CD_a=0.01 #CD at AOA alpha Initial Value
CL_a=0.01 #CL at AOA alpha Initial Value
CM_a =0.1 #Coefficient Aerodynamic overturning moment at AOA alpha Initial Value
Cspin=0.0 #drag coefficient around spin axis
Cmag=0.8 #coefficient magnus force
QM=1.0 #Coefficient
Ix=m*d**2/8 #Moment Inertia x axis
Iy=1.0*10**-3 #Moment Inertia y axis各力がモデリングできたら、timestepに応じて逐次計算をすることで軌道が求まります。4DoF法の強みは、歳差運動周期に対して弾速が非常に早いためタイムステップを細かくせざるを得ず、結果的に適当な一次風上差分でもほとんど誤差が蓄積しない点です。また、deltaxやxなどを目的関数とすれば、目標の未来予測位置に対して狙い位置が定まります。例題ではscipy.optimizeで初期速度ベクトルを求めました。
例題
計算条件
それでは例題でどれほどのズレが発生するか見てみましょう。B-29に搭載された.50口径機関銃を想定して、下記のような諸元を設定します。
| 諸元 | 値 |
|---|---|
| 弾丸口径 | 12.7[mm] |
| Twist Rate*1 | 1/15 |
| 弾丸重量 | 52 [g] |
| 弾丸初速 | 1000 [m/s] |
| 回転減衰率 | 0 (回転数は一定とみなす) |
*1: Twist rate: 1インチ辺りのライフリングの巻数。Twist rate*2π*弾速=回転数 [rad/s]。この事例では、弾丸は158,400rpmで回転していることになります。
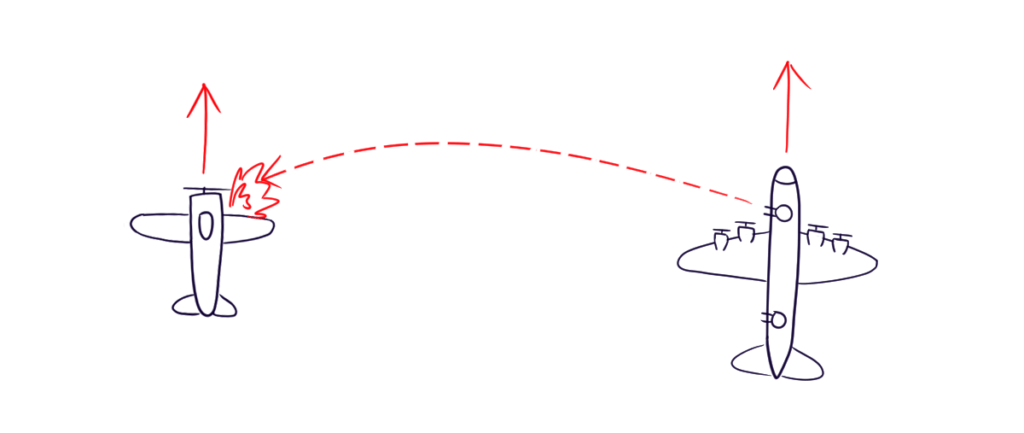
射撃する条件は下記のような状況を想定してみましょう。真横にいる目標に向かって射撃をする場合を考えています。目標と自らは200m/sで前進していて、また目標との距離は真横に400mとします。
| 諸元 | 値 |
|---|---|
| 進行速度 (両者同一とする) | 200 [m/s] |
| 目標との距離 | 400 [m] |
これは戦闘行為というより、警告や威嚇のために接近してきた敵に対して、不意打ちを仕掛けるような状況になるな!
計算結果
FCSから導き出された答えは下記のようになります。横軸のt=0[s]が初期ベクトルで、この初期ベクトルを満たす初速で発射をすることでも目標に命中弾を与えることができます。このような計算結果のことをFiring Solutionと呼びます。またt=0において、xは0、αeも0です。

Firing Solutionの通りに射撃を行った場合、下記のような弾道を描きます。(1/2倍速アニメーションになっています)
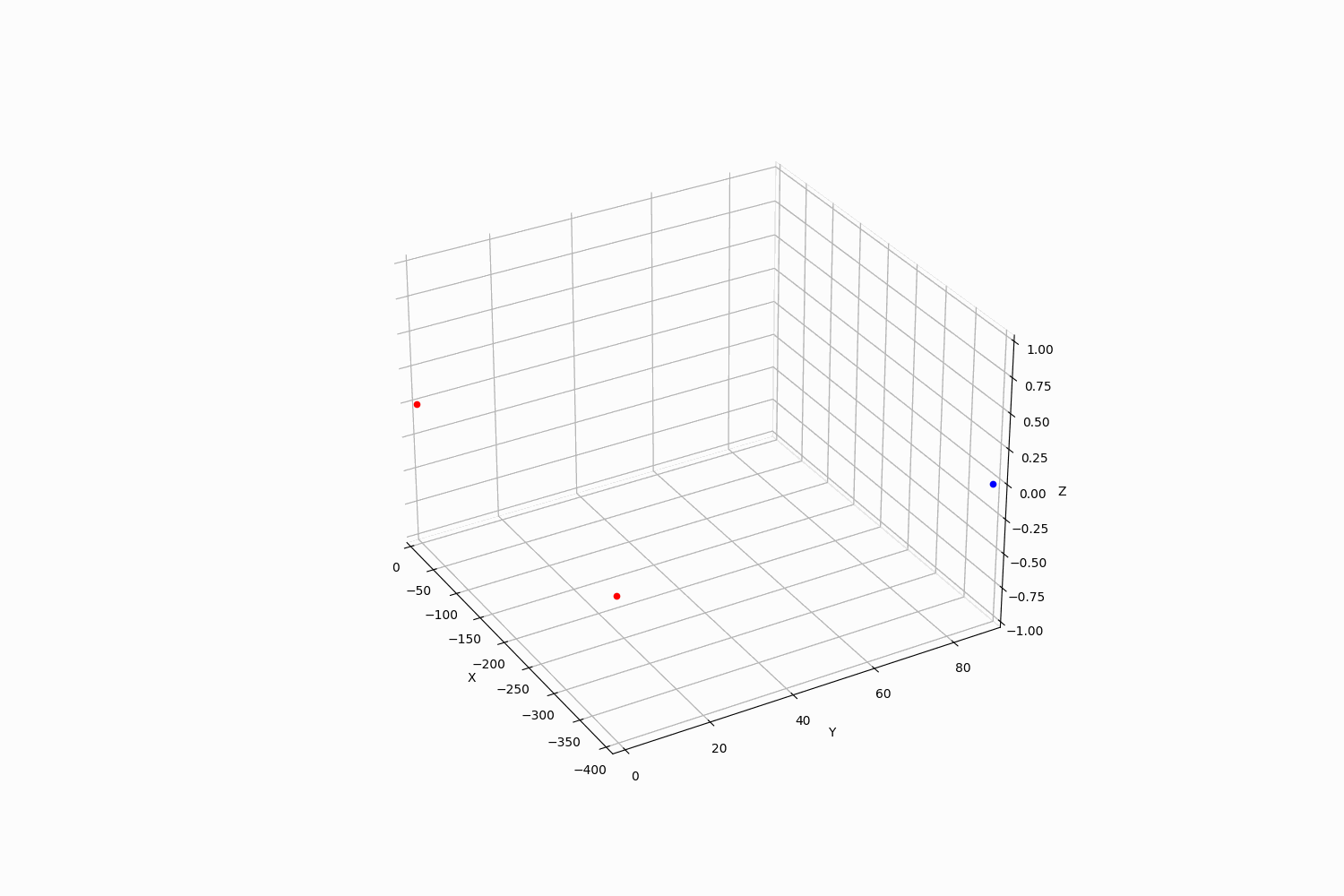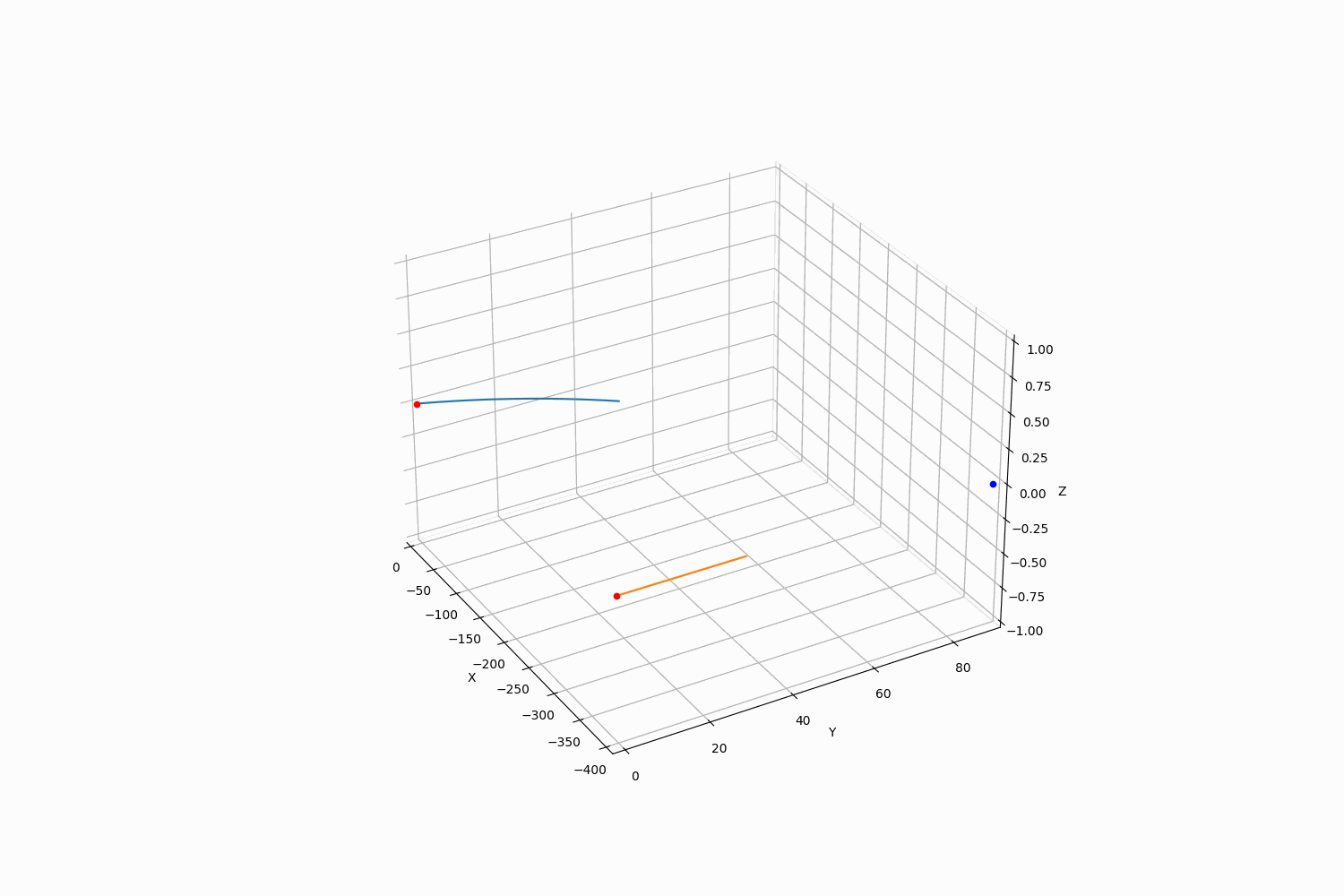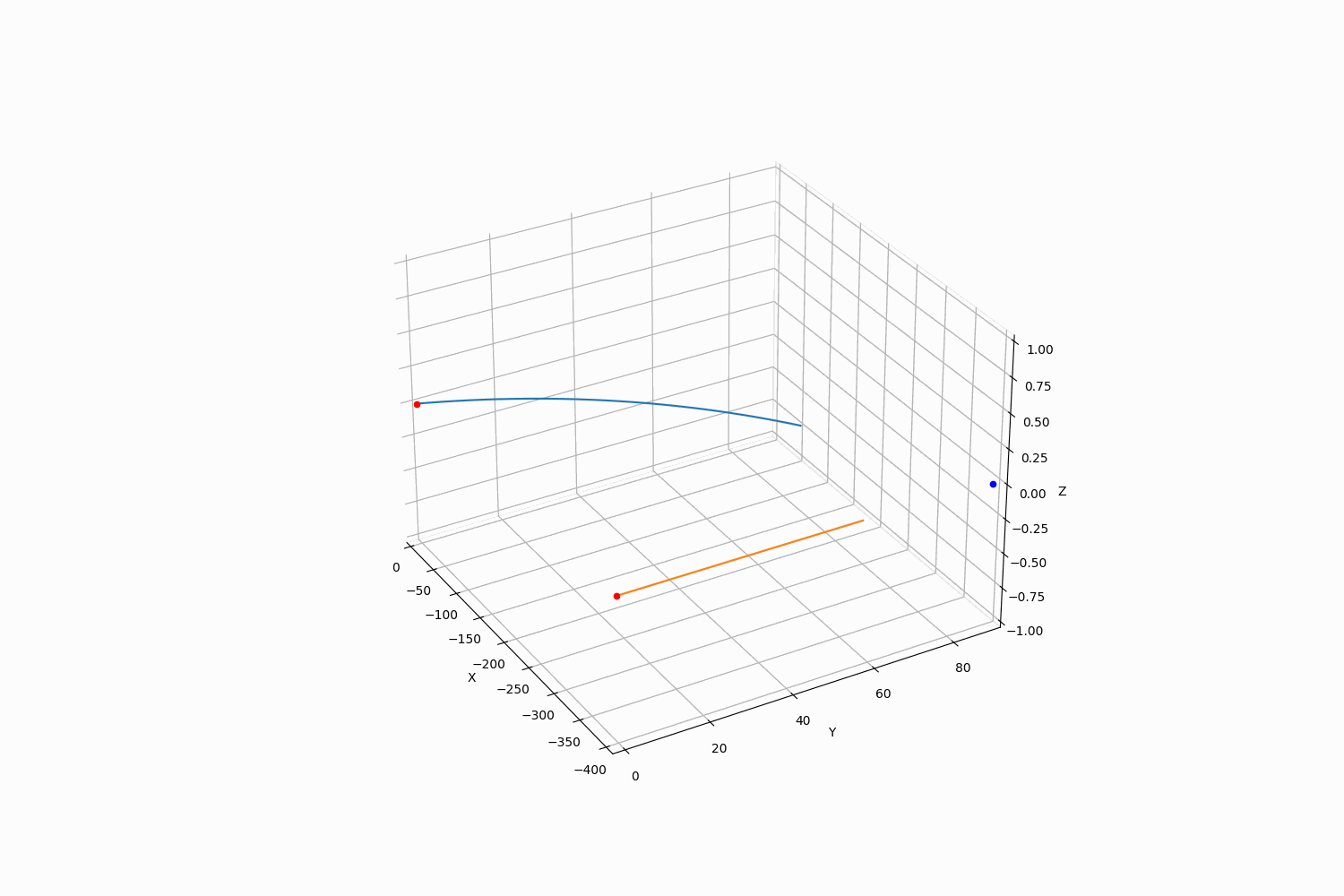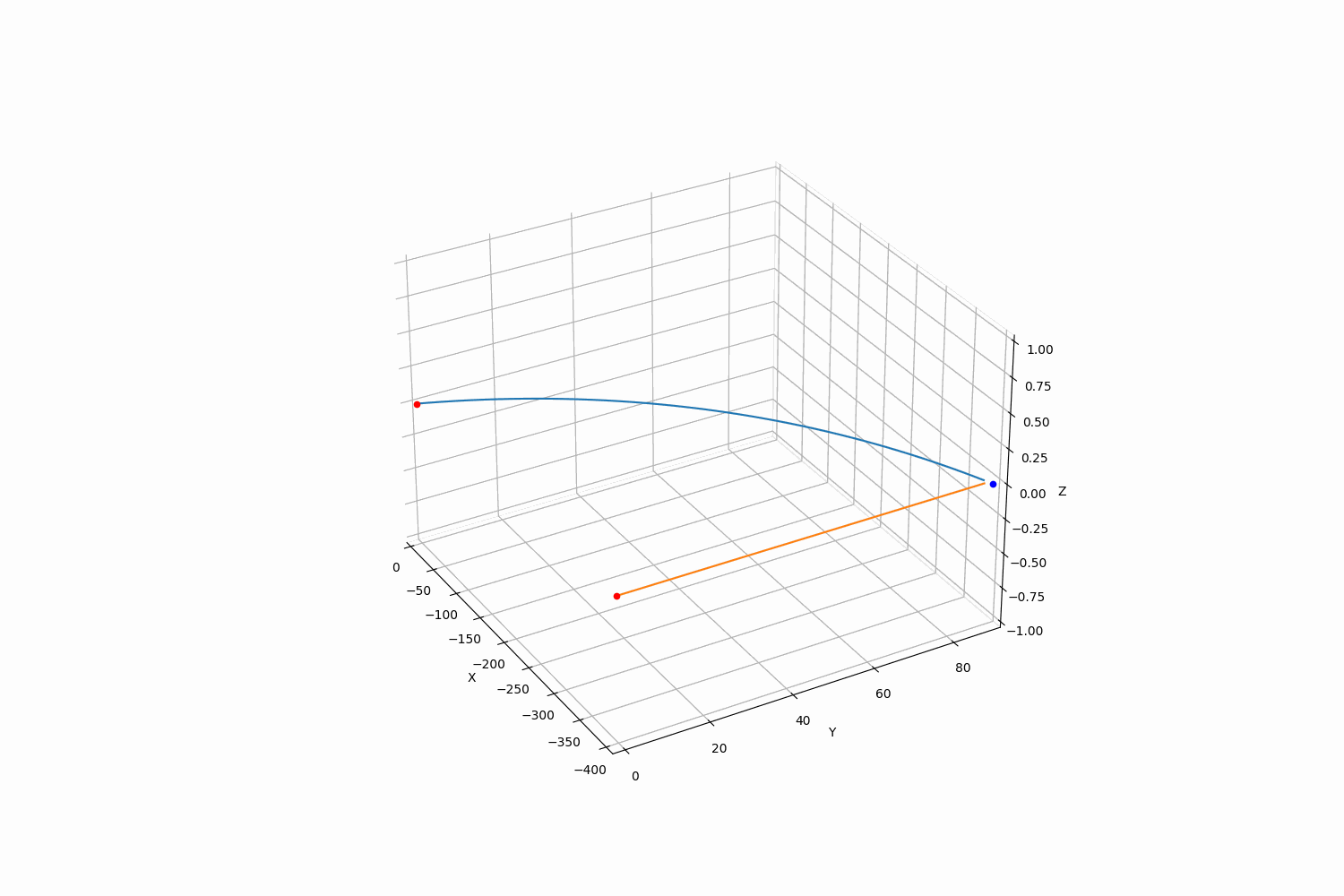
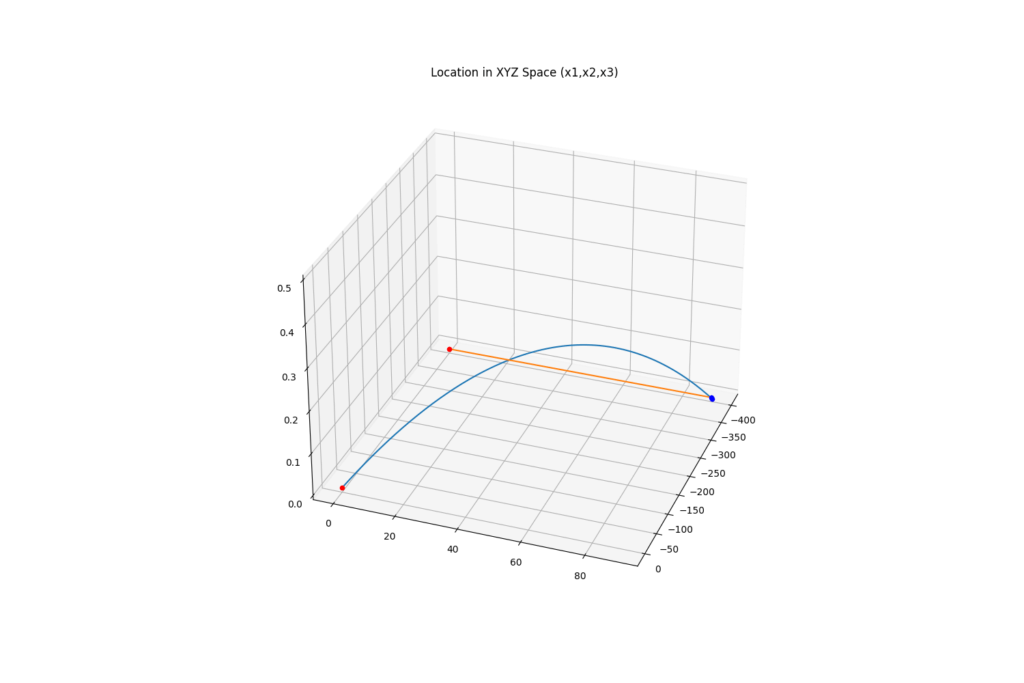
目標との相対位置は下記のようになります。 (delta=0で命中)。非常に高速弾のため、timestepを細かくしなければ計算誤差の関係上完全にゼロには収束しません。
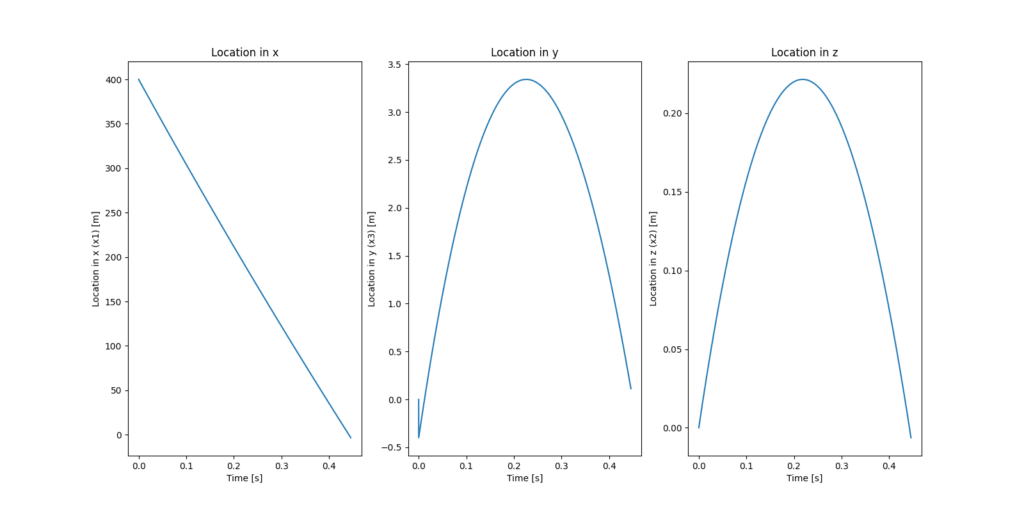
計算結果:
| X | Y | Z | |
|---|---|---|---|
| 位置 x [m] | -405.1 | 90.5 | -0.01 |
| 絶対速度 u [m/s] | -841.5 | 170.9 | 2.00 |
| 射撃角/AOA [deg] | 28.73° | 0.416° |
現代でこそ簡単な計算ですが、当時は初歩的なコンピュータでこのような計算を敵機の情報を逐次アップデートしながらリアルタイム処理していました。
ばらつき影響
次にセンサの不具合で対気速度の読み値が実際から5kt (=2.5m/s)ずれてしまった場合はどうなるでしょうか。ほんのわずかなズレですが、実質的な射撃角度は0.6°もずれてしまい、狙い点からは左右で1.6m、前後で2.9mも離れてしまいます。
| X | Y | Z | |
|---|---|---|---|
| 位置 x [m] | -399.8 | 104.3 | -0.014 |
| 絶対速度 u [m/s] | -828.1 | 196.9 | -2.017 |
| 射撃角/AOA [deg] | 29.32° | 0.413° | |
| ズレ deltax[m] | -2.92 | 1.66 | -0.006 |
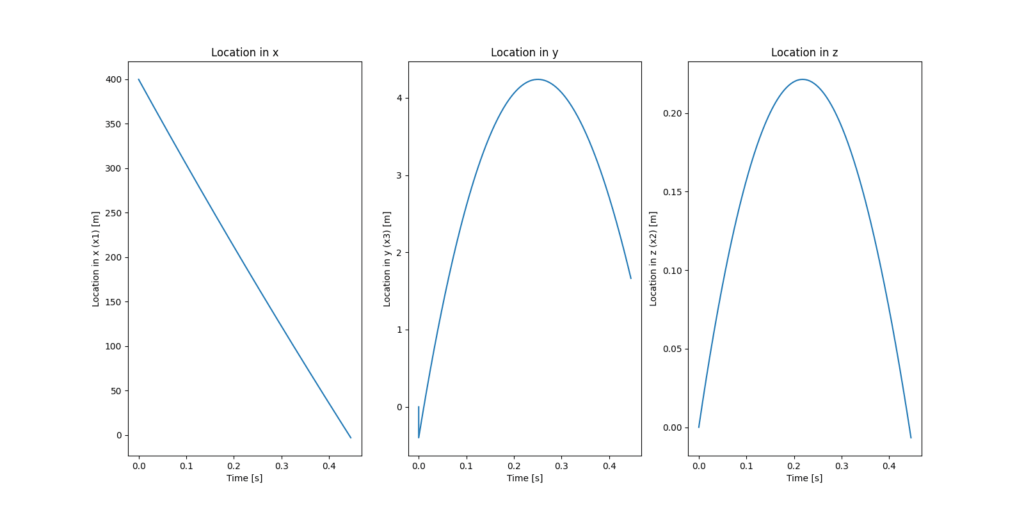
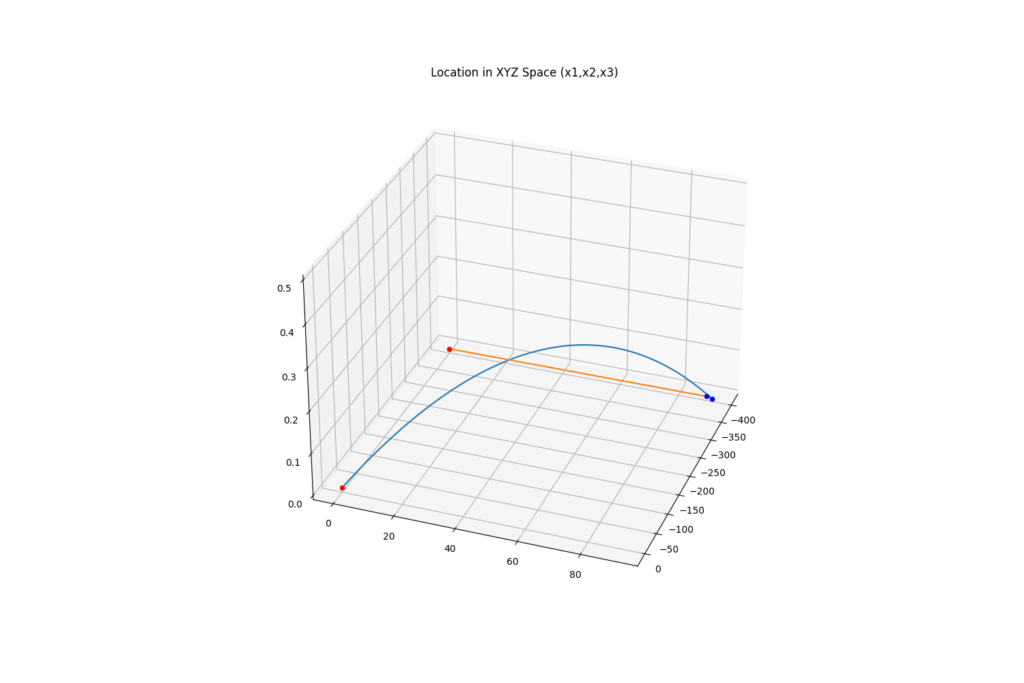
戦闘機の胴体直径は2mにも満たないため、わずか5ktのずれで命中しなくなってしまうことが分かります。射撃精度を維持する難しさはここにあります。
少しセンサが狂っただけで命中しないなんて、使えないって感じるかもしれないが、これでも相当優秀なんだ。人間がやるとどうなるか、次の章を見てみよう。
実はばらつきは必ずしも悪いとは限らないんだ。一発必中の狙撃ならいざしれず、機関砲は連続して射撃をすることができるので、ある程度ばらつきがある場合、狙いが多少外れていても命中する可能性が出てくるんだ。このように位置を少しずつずらした弾丸の雨を“弾幕”と呼んだりする。意図的に狙い位置を上下左右に振ったり、各機銃で狙い位置を微妙にずらしたり、全体として命中率の向上を目指しているんだ。用語は聞いたことがあると思うが、弾幕とはこういう意味なんだ。

感覚で射撃する場合
初心者
FCSを使用せずに初心者が射撃した場合はどうでしょうか。最低限の基礎訓練は終えているとし、重力や風影響はある程度考慮することができ、目標情報を元になんとなく見越角を考えて射撃するとしましょう。なんと50m以上もずれてしまいました。これではまず命中させることはできないでしょう。
| X | Y | Z | |
|---|---|---|---|
| 位置 x [m] | -459.4 | 110.0 | -0.751 |
| 絶対速度 u [m/s] | -774.9 | 200.1 | -3.61 |
| 射撃角/AOA [deg] | – | 0.684° | |
| ズレ deltax [m] | -57.8 | -0.387 | -0.745 |
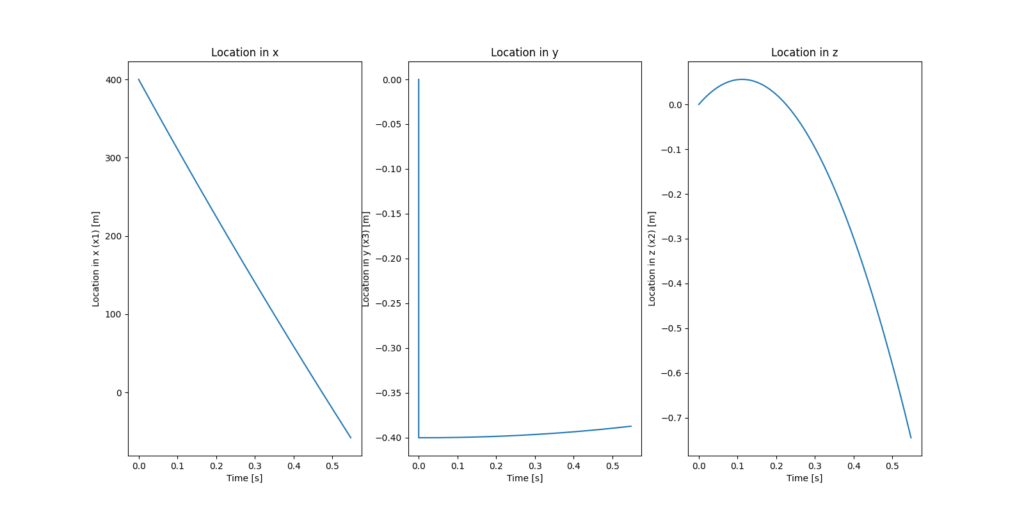
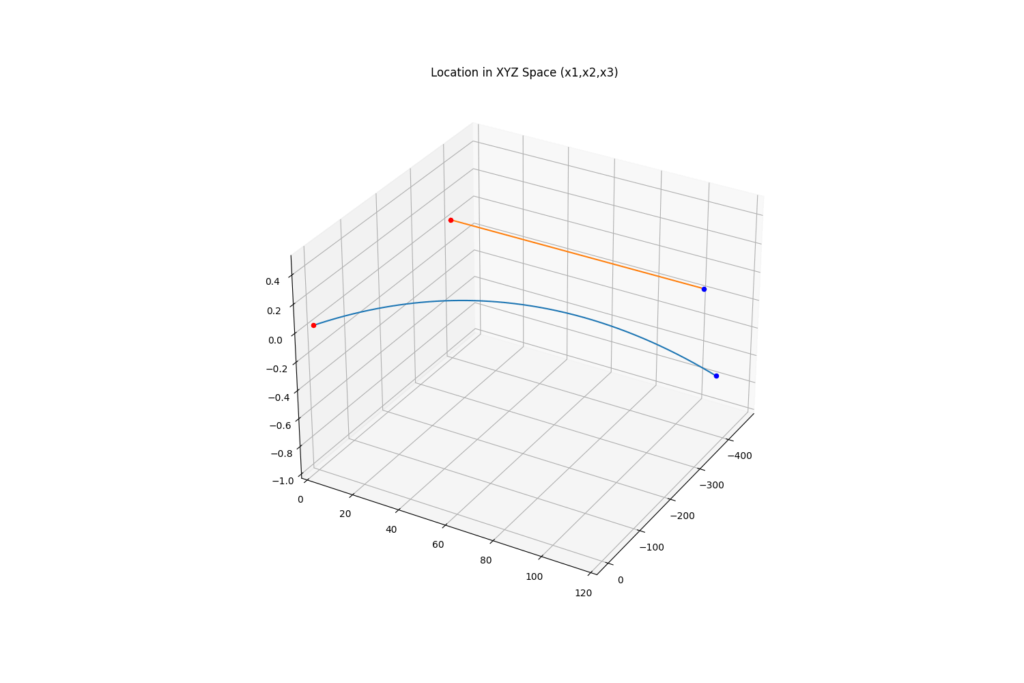
400mしか離れていないのに、50mも外すなんて信じられないようだが、動いている目標に当てるのはそれだけ難しいんだ。むしろ初陣で50m以内に射撃ができたら相当優秀な部類と言える。FCSの存在の偉大さが分かったかな?
熟練
最後に、FCSを使用せずに熟練の射撃手が感覚で照準をした場合です。熟練操作者の場合、マグヌス効果、重力、相対速度は体で覚えていますが、横風や今現在の緯度は知る良しもありません。コリオリ力も揚力もよく分からないので、射撃練習場で体に叩き込んだ経験をベースに射撃することになります。
結果は20m以下と、非常に惜しくなりました。また時系列で見ると、タイミングが少しずれて外してしまっているものの、タイミングがあえば命中していた可能性があります。たくさん打てば命中するかもしれない水準です。FCSには及ばないものの、まだまだ勘頼みの射撃でも通用する場合もあったことが分かります。
| X | Y | Z | |
|---|---|---|---|
| 位置 x [m] | -404.6 | 91.6 | -0.011 |
| 絶対速度 u [m/s] | -840.4 | 173.7 | -2.002 |
| 射撃角/AOA [deg] | 29.32° | 0.413° | |
| ズレ deltax [m] | -15.5 | 1.66 | -0.06 |
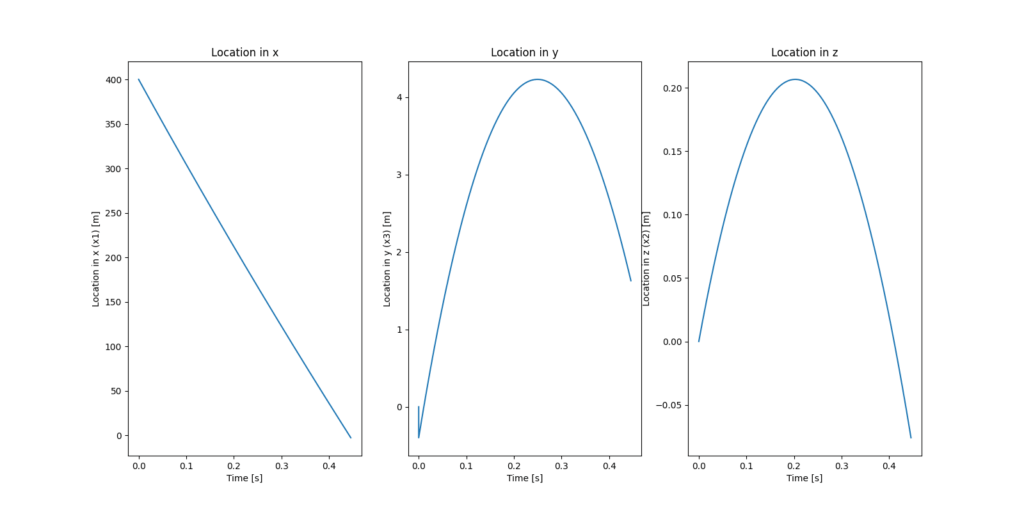
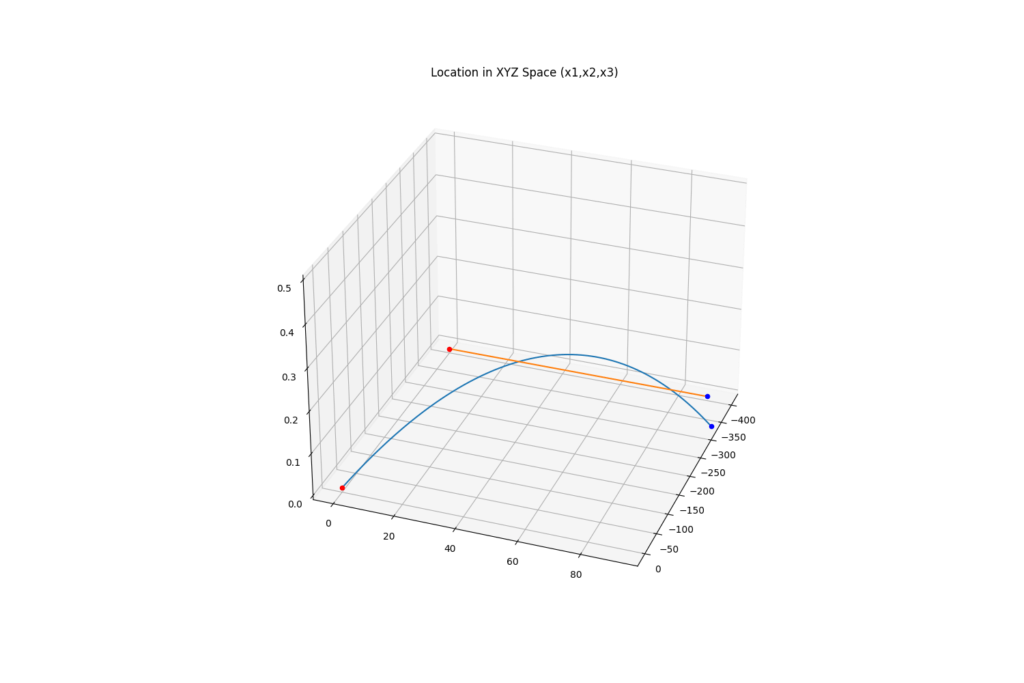
命中確率を計算する時は、ここで行ったような誤差を仮定して、様々な誤差の組み合わせを総当り的に計算する、モンテカルロ法がよく用いられるんだ。その計算の最終結果が“命中精度”と呼ばれていて、数多くの射撃試験を行ってはじめて本当の命中精度を確認することができるんだ。
理想に対してばらつきを入れたFCS、初心者、熟練それぞれの命中精度はどうでしたか?MPMTMは本来砲弾の計算用なのですが、今回はFCSが最も活きる、自分自身が移動している場合の移動目標に対する計算で紹介をしてみました。
最後に
本日はここまでです!砲術入門後編としてMPMTMを紹介しましたが、規格を使えば複雑な砲弾の運動も簡単に計算できること、また、B-29の先進性とFCSの偉大さを知ってもらえたなら嬉しい限りです。
今は武器や訓練が進歩しているけど、当時同じ装備で戦ったらぼくは勝てる気がしないよ、、、昔の人はすごかったんだなってつくづく思うな!
ここまで読んでくれた方は、本当にありがとうございます!たまにはこういうのも書きたいと思うので、また楽しみにしていてください!
*この記事では説明や計算の簡素化を目的にSTANAG規格上の仕様のすべては実装していないため、若干の誤差があります。本来の計算に興味を持った方や、詳細が知りたい方は、是非原文を入手してみてください!
それでは、また次回お会いしましょう!
参考・クレジット
https://ja.wikipedia.org/wiki/%E7%90%83%E9%9D%A2%E5%BA%A7%E6%A8%99%E7%B3%BB
https://www.nennstiel-ruprecht.de/bullfly/
https://ja.wikipedia.org/wiki/%E3%82%B3%E3%83%AA%E3%82%AA%E3%83%AA%E3%81%AE%E5%8A%9B
https://www.researchgate.net/publication/327582502_Calculating_Yaw_of_Repose_and_Spin_Drift
https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.885.7614&rep=rep1&type=pdf
https://infostore.saiglobal.com/en-gb/standards/stanag-4355-0-736122_saig_nato_nato_1787963/
https://qiita.com/MuAuan/items/a05a9823345ff75251ff
https://www.mod.go.jp/atla/nds/Y/Y0006B.pdf
https://press.hornady.com/assets/site/hornady/files/ballistic/hornady-4dof-technical-paper-v2.pdf
https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/11-3-precession-of-a-gyroscope/#:~:text=The%20precessional%20angular%20velocity%20is%20given%20by%20%CF%89P%3Dr,frequency%20of%20the%20gyroscope%20disk.