【流体力学】風力で時速200キロ。空力の最先端：アメリカズカップヨットとセイルカー

Contents

ヨットを速く走らせてみよう

最大速力の計算手順

先章の模式図と公式を元に、最大速力を求めてみましょう。

セイル迎角α、セイル開き角度ξの最適値を求め、結果的にスリップ角βが得られます。2変数の最適化問題ですが、数学が苦手な方でも三角関数さえ分かれば大丈夫です。
古典的なやり方で、線図を引いてアナログ的に解いて行きましょう。

計算を行う際、不明な定数がいくつかあります。これはヨットの諸元で決まるものですが、ほとんどの場合は見積もりができるため、下記のように仮定して計算してみましょう。特殊な翼型や特性がわかっている翼型の場合は揚力係数・抗力係数を実際の取得値に合わせて入れてくださいね。

計算手順

\( CL_s \propto \alpha \) ：セイル揚力係数はセイル迎角に比例する
\( Cd_s \propto \alpha \) ：セイル抗力係数はセイル迎角に比例する
\( CL_k \propto \beta \) ：キール揚力係数はハルスリップ角=キール迎角に比例する
\( Cd_k \propto \beta \) ：キール抗力係数はキール迎角に比例する
ハル抗力係数は通常船型の場合は一定、フォイリング船の場合はキール迎角に比例するものとする。

任意の風向きに対する最大速度の計算手順は下記の通りです：

計算手順

各諸元：(セイルやキールの揚力・抗力係数、面積、ハルの抗力係数等)が決められたヨットが、風向きに対してθの角度で進んでいると仮定する。
セイルの迎角αを仮定する。
式①、③、⑤、⑧よりセイル横力Ssとキール揚力Lkの横方向の力の釣り合いを求める。
式②、④、⑥、⑦よりセイル推進力Tsとキール抗力dkとハル抗力dkの合力の釣り合いを求める。
上記作業を行うことで、釣り合いが成立するβが得られる。
式⑨、⑩のベクトルの和より見なし風速vsが上記より得られたハル速度vhと一致するか確認する。
成立しなかった場合、ξを操作して、再度3.から計算する。
新たなセイル迎角αを仮定し、2.～7.を計算する。
もっともハル速度vhが速くなるα、β、ξの組み合わせが得られたら完了。

上記の作業を行うと、このように複数の釣り合い線が得られます。しかし解析解がないため、実際にはいくついかのβとξのパターンを試して、成立点を探す必要があります。下図は仮に風速vaと迎角αを固定し、セイル開き角ξを7～10°まで振ってみた場合の見なし風速です。釣り合いが得られていない状態では、力の釣り合いとベクトルの釣り合いは成立していないので、下記のように仮定値を設けています。：

va：風速。ここでは10[m/s] 一定としている
θ：進行方向は20°で一定としている。
α：セイル迎角。下は6°の場合の線図
vs1：④過程において、推力の釣り合いが得られていると仮定した場合の見なし風速vs
vs2：⑥過程において、ベクトルの和が成立していると仮定した場合の見なし風速vs (vs1とは一致しない)
vsb：③過程において、横力の釣り合いが得られていると仮定した場合の見なし風速 vs
vh：ハル速度vh

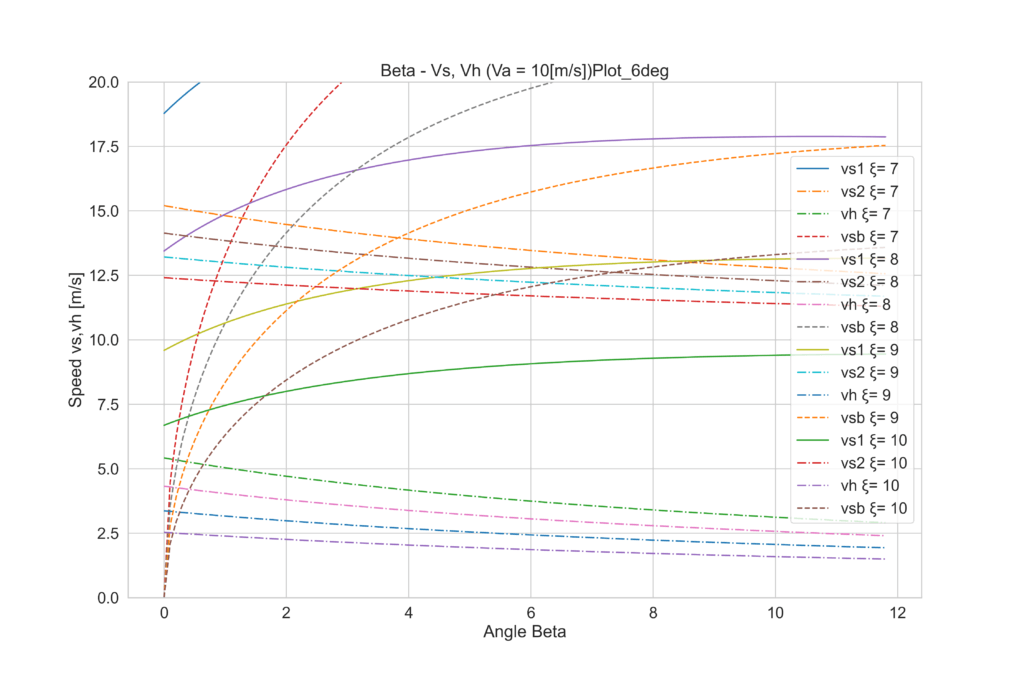
(zzzzzz……)

あ、またかずおが寝てる、、、
この図だとちょっと線が多すぎてわけがわからないかも。結局βとξを求めればいいんだっけ。。。？

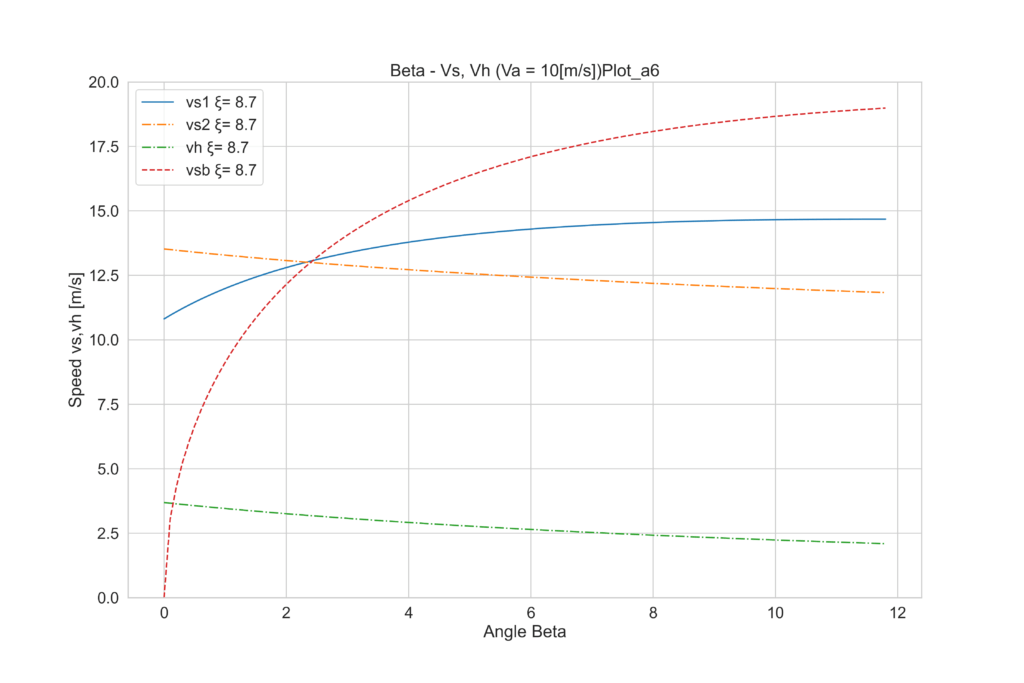
たしかにこの図だとちょっと難しいですが、見てほしいのは、ξをいじると、同じβでも各線が上下している点です。vs1、vs2、vsbそれぞれがξによって動いているが分かりますか？簡素化のために、答えが出ている状態のξで同じプロットをもう一度見てみましょう。

あ、これならわかった！α=6°の場合は、ξを8.7°にすると、βが2.3°ぐらいにで釣り合いが得られて、速力は3.2m/sぐらいになるってことだね。

入力する値によっては、成立解が得られない場合もあり、その場合はヨットはその方向には進めないということを意味します。仮にθ=0°などと設定して試してみると面白い結果が得られます。

演習：最大速度が得られるαを求める

それでは実際に速度を計算してみましょう！仮諸元として、通常船型のかなり高性能な個人用の小型ヨットを仮定して、下記のような無次元パラメータを仮定します。先程の図をそのまま使ってしまいましょう。

演習ヨットの諸元

\( \frac{A_s}{A_k} = 20 \) セイルキール面積比
\( \frac{A_s}{A_h} = 4 \) セイルハル面積比
\( L/D_s = \frac{CL_s}{Cd_s} = 20 \) セイル揚抗比
\( L/D_k = \frac{CL_k}{Cd_k} = 20 \) キール揚抗比
\( Cd_h = 0.05 \) ハル抗力係数
\( \rho_a = 1.2 [kg/m3] \) 空気密度
\( \rho_w = 1000 [kg/m3] \) 水密度

この諸元でαを2～7°の間に振ってみましょう。

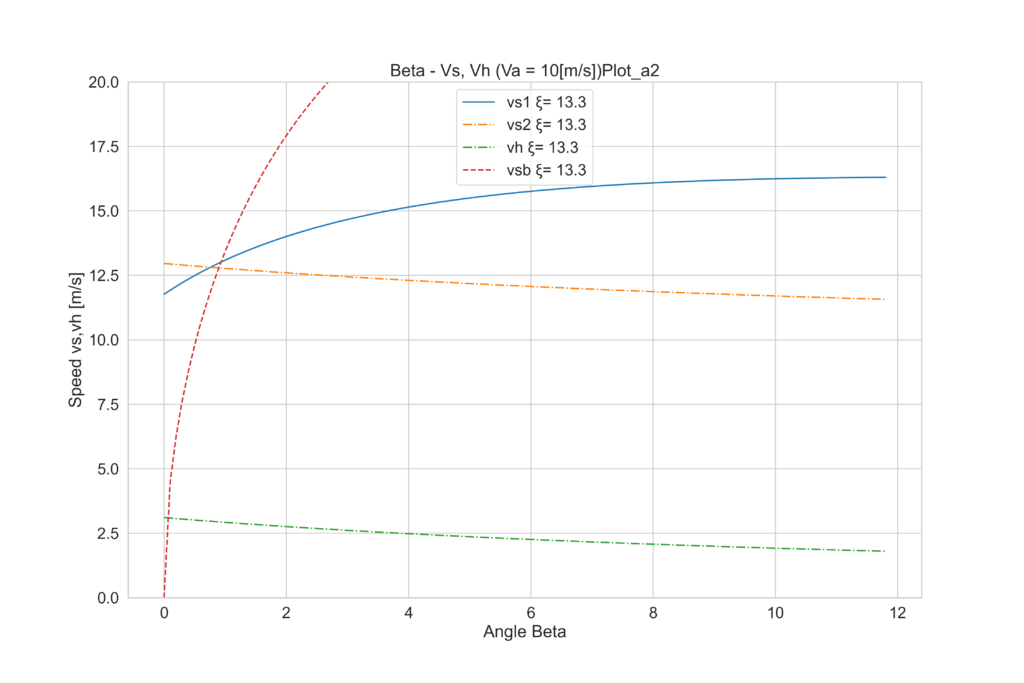
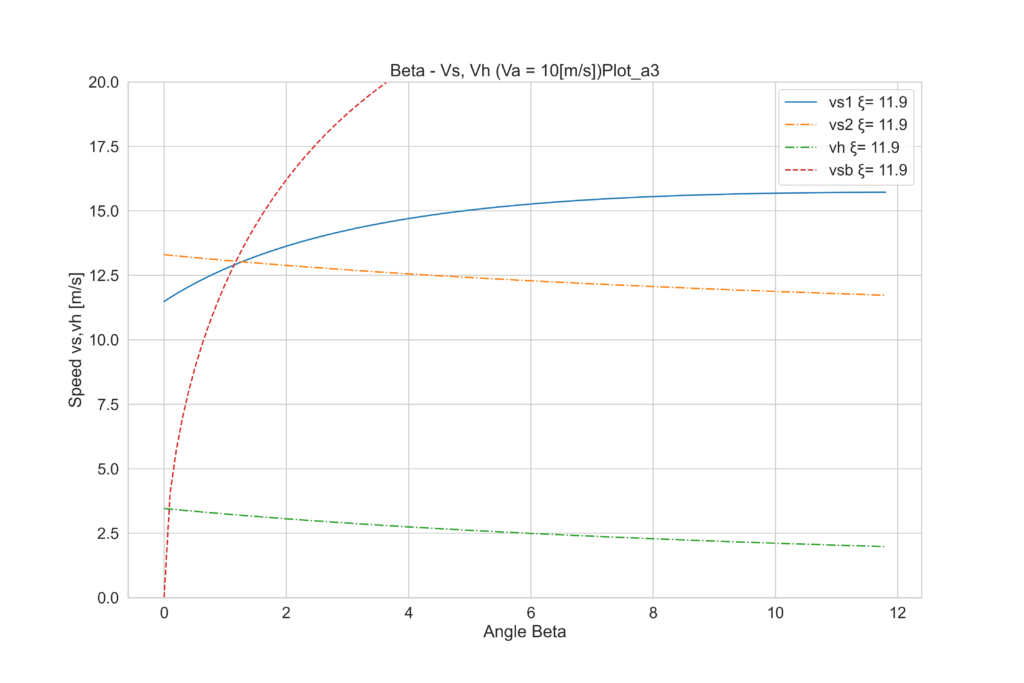
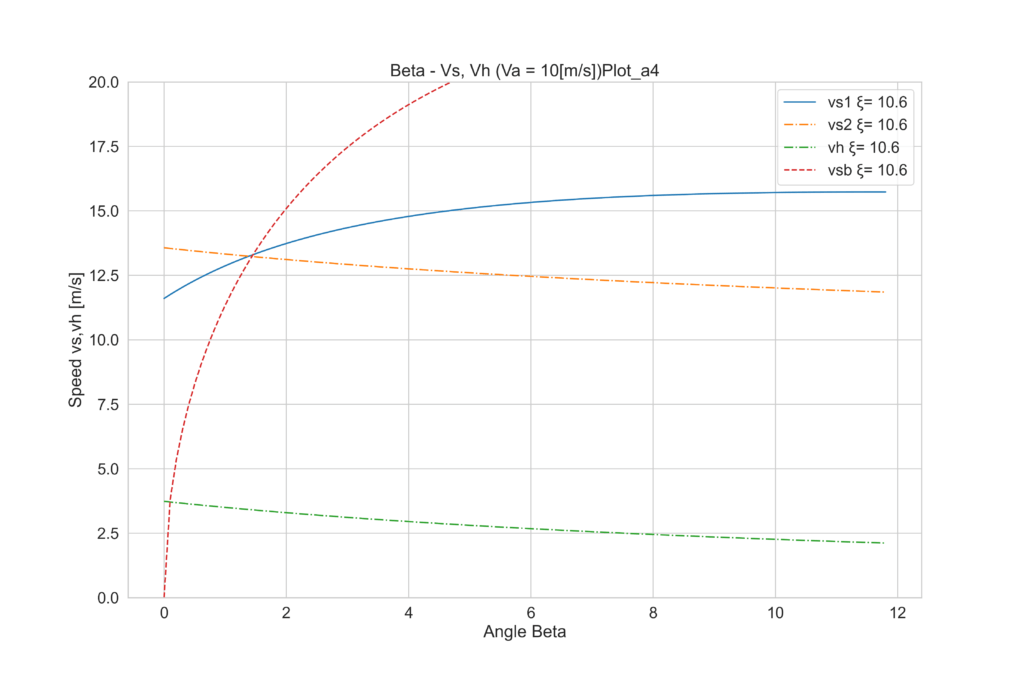
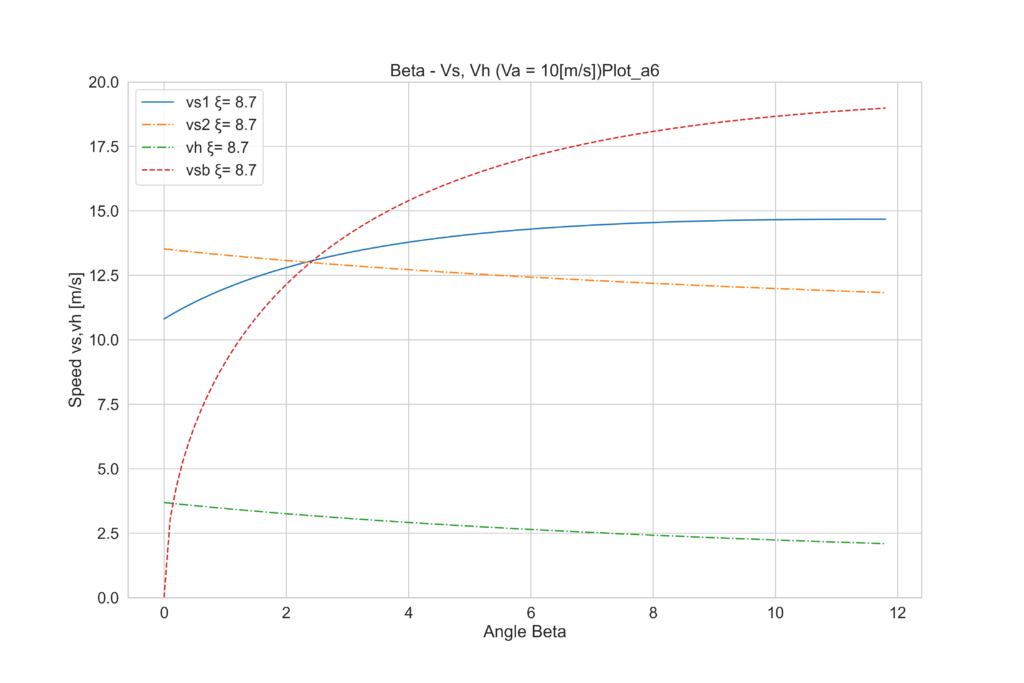
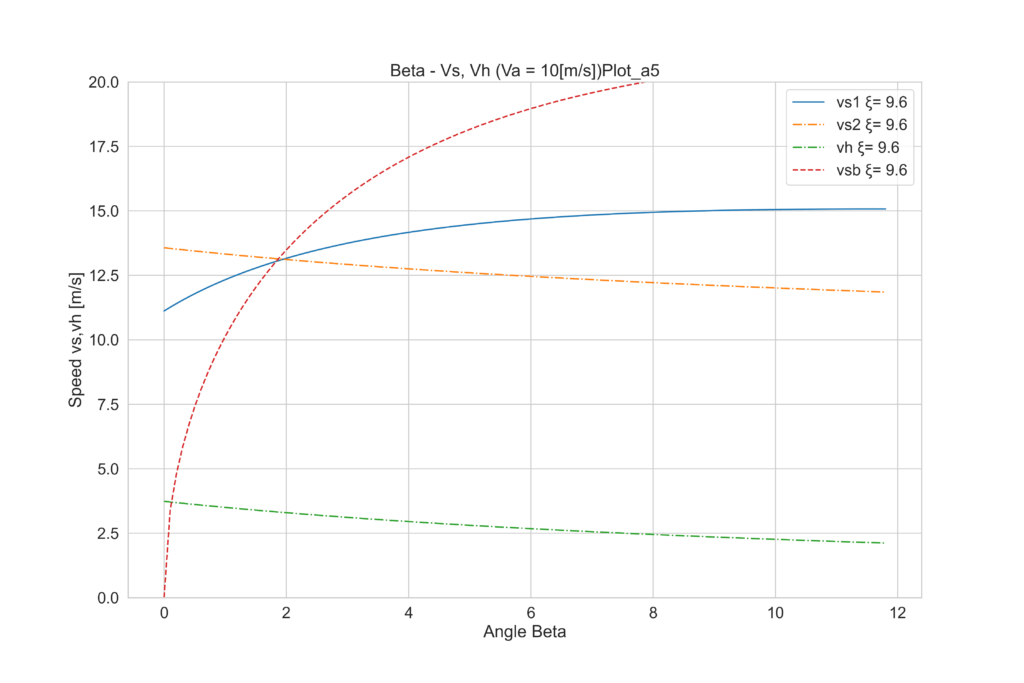
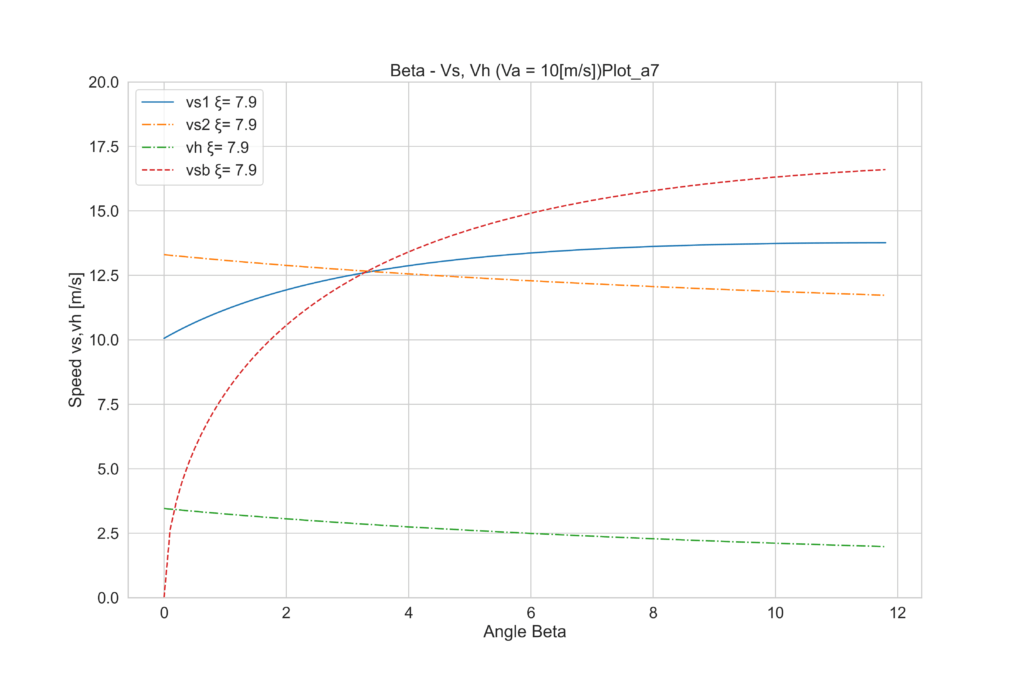
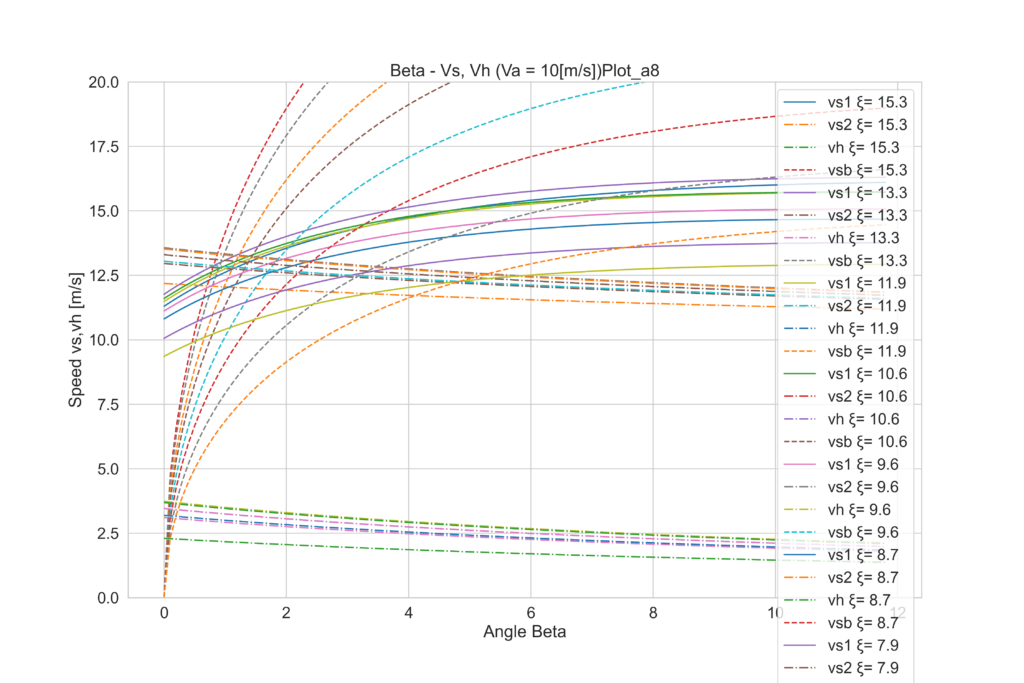
全部見比べると、2°からαが増加するにつれて、vhは増加するものの、4°付近を最大にに、5°以上では再び減って行くことが分かります。つまりこのヨットの場合は下記のことが言えます。

Va = 10 m/s、θ=20°の場合の最適セイル角

Va = 10 [m/s]、θ = 20°において
α=4°
ξ=10.6°
β=1.75°
上記において、最大速力vh=3.6 [m/s]が得られる。

風速の約1/3かぁ、イマイチ遅いなぁ

そうですね、いくら高性能な船体とは言え、θ=20°ともなるとほとんど風上に向かって進んでいることになるので、あまりスピードは望めません。しかし行きたい方向が風上の場合は仕方ありませんよね。
それでは、みなさんはどの角度が一番有利だと思いますか？

最大風速が得られるθは？

いきなりネタバレですが、ハル速度vhが最速となる進行方向θは90°です。

*↑2021/9/6更新：有識者の方から指摘があり、必ずしも90°とはなりません。セイルにより多くの風を当てるという観点では0~90の状態が最も揚力が得られますが、最適角度はハルやセイルの特性によって変わってくるため、それぞれの角度で検討をする必要があります。

先程と同様の手順で、90°と120°それぞれの場合を見てみましょう。

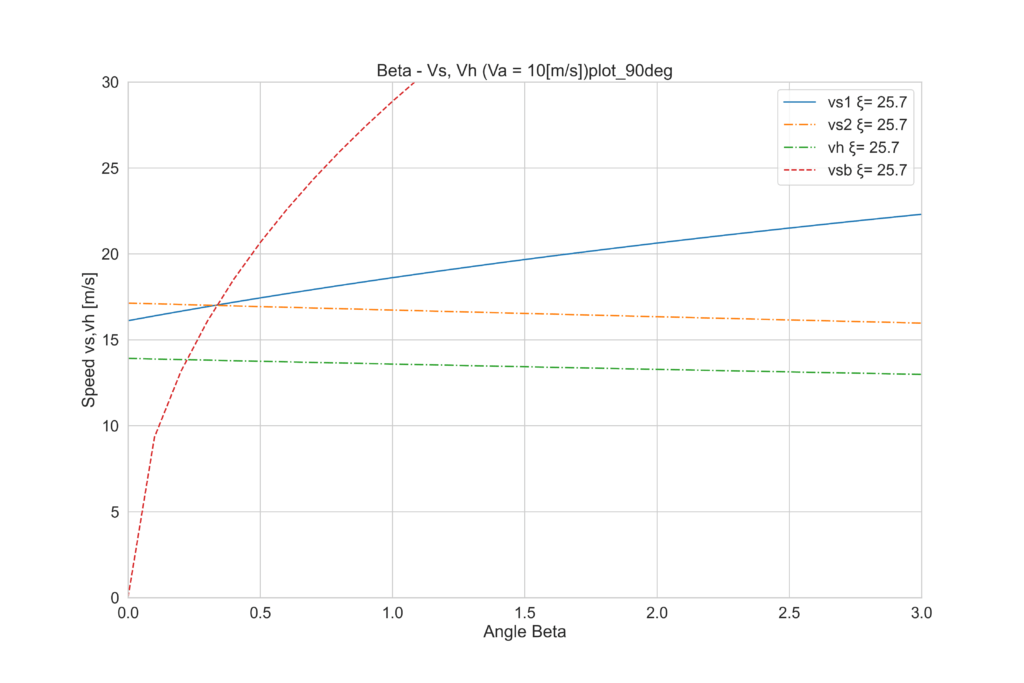
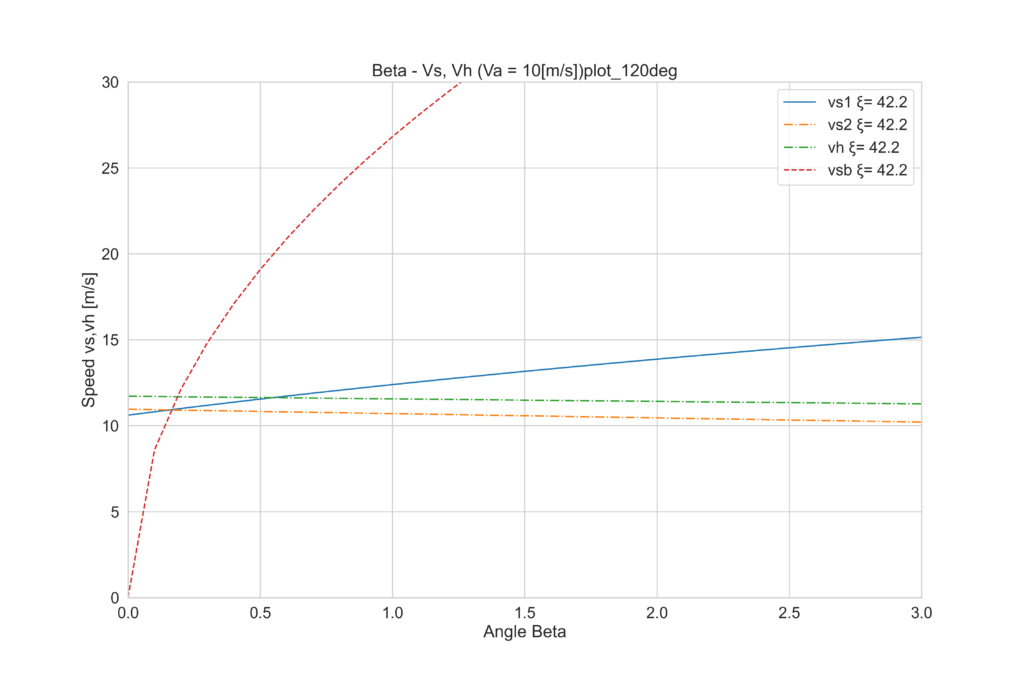
θ=90°ではvs=17[m/s]、vh=13[m/s]と、風速va=10[m/s]以上の速度で進めることが分かります。

θ=120°になると風下にセイリングしている状態でvh>vsとなり、風速よりも、見なし風速よりも速く走ることができます。しかし実際の速度自体はvh=12[m/s]と、90°の時には敵いません。

このようにスキッパーは常に狙った進行方向に対して最適なα、ξを調整しており、更にはキールを動かすタイプのヨットではβも調整しています。
また進行角度θも、目的方向に一直線に向かうよりも遠回りしてでも速力を優先したほうが速い場合が多く、コース取りがレースでは勝敗を決します。

見極めは非常に難しく、長年の経験と勘が頼りになりがちです。飛行機の操縦よりも難しい、とよく言われます！

考えることが多い！セイリングが奥が深いってことはよくわかったよ

風速よりも速く走れるってスゲェよなぁ。インーインーインの最短距離重視のラインを取るか、最速ボトムスピード重視のラインを取るか、ヨットレースにも色んな攻め方があるんだな。

このように、ラダーを使わなくてもセイルを上手に調整すれば好きな方向に最大速度で進ませることができるということがよく分かります。

ここでは、ヒールのバランスについてはあえて触れませんでした。なぜなら双胴船と単胴船、フォイル船と一般船ではバランスのとり方が全くことなり、多くの場合船体の安定性に影響を及ぼしても、抵抗にはそこまで大きな影響とならないためです。小型のディンギーヨットなどでは乗組員の重心移動だけでバランスを維持するため、水平を保つのが難しく、ヒール状態を前提に傾いた時に最大推進効率が得られるように設計されているものも少なくありません。

アメリカズカップ並の超性能のヨットを作る

超高性能ヨットを作るにはどれぐらいの諸元が必要なのでしょうか？実際のアメリカズカップのヨットは風速の4倍の速度で航行可能と言われています。先程の手順で諸元を仮定して計算してみましょう！

演習ヨットの諸元

\( \frac{A_s}{A_k} = 20 \) セイルキール面積比
\( \frac{A_s}{A_h} = 60 \) セイルハル面積比
\( L/D_s = \frac{CL_s}{Cd_s} = 20 \) セイル揚抗比
\( L/D_k = \frac{CL_k}{Cd_k} = 10 \) キール揚抗比
\( Cd_h = 0.001 \) ハル抗力係数
\( \rho_a = 1.2 [kg/m3] \) 空気密度
\( \rho_w = 1000 [kg/m3] \) 水密度

フォイリング船ではハルが水に接触しないため、セイルとハルの面積比があり得ないような値に設定することができてしまいます。フォイルの分の抵抗は増えるものの、キールにかかる横力と比べると船体の重量はそこまで大きくはありませんので、抵抗としては最小限の増加にとどまります。(ただしCFRPで極限まで軽量化した競技用ヨットに限っての話になります。)

それでは同じく風速Va = 10[m/s]、角度はθ=100°と仮定して線図を引いてみましょう。

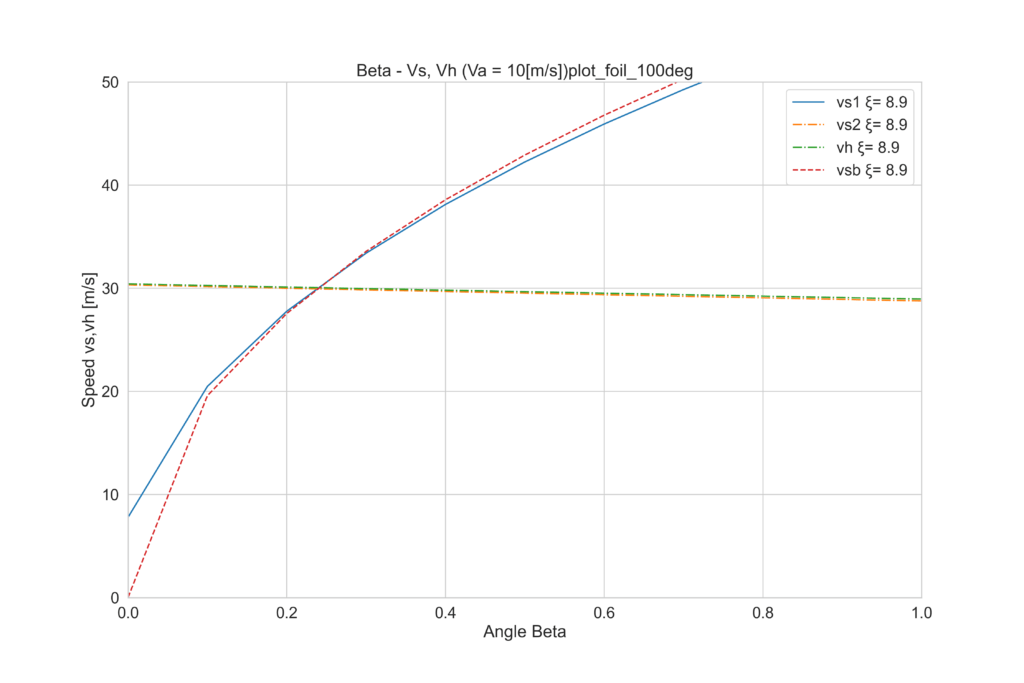
なんと、Vh=30[m/s]も発揮され、ほぼvs=vhとなりました。

風速の３倍！！時速100キロ超え！やば！！！

やっちまった感が否めないですよね、、、フォイリング船は形が似ているだけで全くの別の乗り物と考えたほうが良さそうです。
揚抗比20となると、最新鋭のジェット旅客機よりも優れるレベルで現実には達成は難しいと思います。
恐ろしいことに、アメリカズカップのヨットは風速の4倍、つまりこれよりも更に効率が良いのです。。。空力を志す者、一度は見てみることをおすすめします！

*アメリカズカップのヨットはフォイルだけでなく、船体自体が翼面形状となっており揚力を発生させるため、実際にフォイルが必要な揚力=迎角が非常に小さく、通常ではあり得ない抗力の低さを実現しているためこのような芸当が可能になっています。セイルの代わりによりパワフルなエンジンを搭載し、この原理で海上を時速500キロ以上で移動する乗り物、エクラノプランというものもあり、また別の機会に紹介したいと思います。

恐ろしいスペックのヨットが出来上がってしまいましたが、時速200キロにはまだ届いていません。記事のタイトルは嘘だったのでしょうか？

時速200キロ。世界記録の樹立

ここまで読んで頂いて、ACヨットの更に2倍の最高速を出すためにはもっと抵抗を減らさないと、、、船体なんてなくして車輪をつけちゃおう！という発想に至った方もいるかもしれません。

まさにそういう乗り物があり、ランドセイリング：陸上セーリングという命知らずの人たちのための競技が存在します。

実は最も速いセールによる乗り物は、陸上を走るGreenbirdです。なのでヨットではありません、しかし風の力だけで走ることは同じです。

風の力だけで時速200kmが出せるのもすごいですが、命がけすぎて観てるだけでドキドキしてしまいますよね。。。！ハルやキールをなくし、代わりにタイヤで横力に耐えるため、フォイルよりも更に抵抗を減らすことができ、まさに究極の風力で動く乗り物となっています。

ここまで読んでくれた方は、どうやったら時速200kmが出せるか検討してみるのも面白いと思います。

オンボードがアタマオカシイわね、、、りゅうたにぴったりじゃない！乗っておいでよ

う、、、オ、オレはいいや、、、ヨットは初心者だしな！ビビってるわけじゃねえからな！

本日も最後まで読んで頂きありがとうございました！ヨットに少しでも興味を持ってくれた方、自分はスピード狂だと気づいてしまった方、楽しんで頂けたなら嬉しいです。身近な自然の力をうまく利用することで、常識外のことができてしまう、こともまた物理の面白いところだと思います。

参考・クレジット

翼と揚抗比について：

ヨット理論の詳細:

Science of the 470 Sailing Performance

ヨット研究の第一人者によってオリンピック種目である470型について非常に入念に調査されていて、ヨット理論はすべてが詰まっていると言っても過言ではないです。個人的に超おすすめです。
この記事ではヒール(ロール)のバランスやピッチの影響など、尺の都合上実際のセイリングで重要な要素を省略していますが、もっと知りたい方には一番のおすすめ文献です。

ヨットの仕組みやセーリング技術についての参考記事やおすすめ図書です：

ヨットの専門サイト：
Hirosite

ヨット関連ニュース:
バルクヘッドマガジン　

ヨット関連ニュース:
セーリングの入門書・ディンギーセーリング　

1 2