はじめに
おいおいおい、いきなりわけのわかんねえカタカナが出てきたよ。もう帰ろうかなぁ
ちょっとだけ待ってください!いきなり“ローターダイナミクス(RD)”なんて聞くと???ってなると思います。
でもRDとは、回転するあらゆる物体に影響を及ぼします。現代文明において最も重要な科学分野の一つ、と言っても過言ではありません。
RDが無くては、水道や電気と言った回転機械を使うインフラはもちろん、パソコンや自動車のような近代的な機械はほぼ成立しません。
本日はそんなRDについて、難しい数式を使わず、なるべく分かりやすく、その重要性と考え方について解説をしたいと思います!
今回は”入門編詐欺”じゃなくて、”本当の入門編”だ。これを読めば、必ず理解ができる!少しでも機械に興味があれば、読んでおくことをおすすめする!
- ローターダイナミクス(RD)って何?
- 乗り物や機械に興味がある
- 近代文明を支える基本理論を知りたい
- 今回の記事のレーティング:
回転体のバランスとは
世の中には回転する物体がたくさんあります。タイヤや駒、そして地球から微粒子まで、大抵の物体は回転しています。業界用語では、これら回る物体のことを“回転体”と呼んだりします。中でも軸を有するものはあらゆる回転部を持つ機械で使われています。

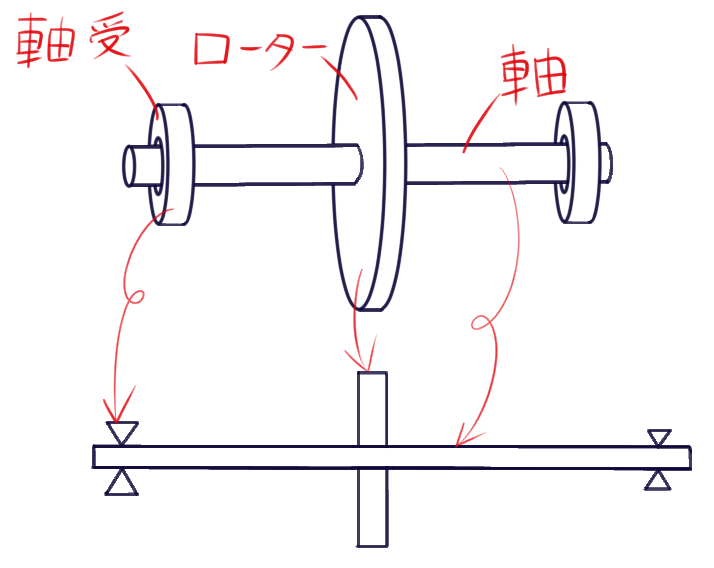
軸の構成要素
軸は主に4つの要素から構成され、合わせて“軸系”と呼びます。
- 軸:各部品が取り付く大黒柱のようなもの。これを中心に回転します。
- ローター:軸に配置される重量物、インペラやフライホイールなど
- 軸受:軸の回転を支えるベアリングのこと
- 支持構造:ケーシングとも。軸受を支える構造体です。地面で直接支持する場合もあります。(図には入れていません。)
駒の動きと軸の動き
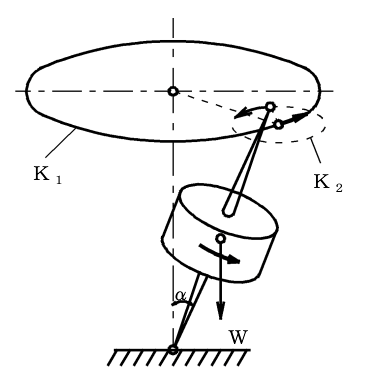
駒やベイブレードの運動を想像してみてほしい。綺麗に芯の周りで回るだけでなく、少しふらふらとしながら回っていることに気づくだろう。
多くの物体は、よく観察すると駒に似たような動きをするんだ。これを“歳差運動”と呼んだりする。歳差運動は単純な円を描くだけでなく、複雑な模様を描く場合もあるが、ほとんどの場合は円の組み合わせだ。
太陽の回りを回る地球、そして地球の回りを回る月、これに似たような動きをイメージすると分かりやすい。
同じような現象が、支持された軸でも起きます。これを“振れまわり”や“ホワール”と呼び、振れまわりを含む軸が動き回る現象のことを“軸振動”と呼んだりします。
このように不釣り合いがある軸では、振動が発生し、軸全体の動きに影響を及ぼします。
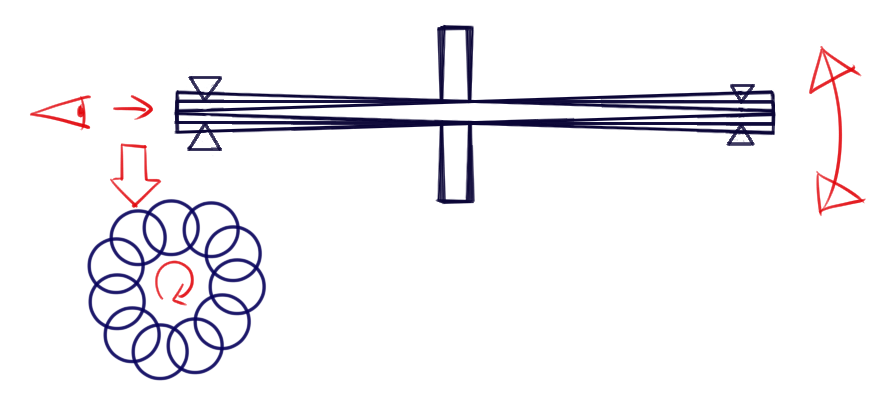
上の図では、軸が振動している状態です。このような状態の軸を左側から見ると、軸が円を描くように駒の頭のような運動をします。これは代表的な振れ回りの動きの一例ですが、軸は他にも様々な動きをします。
回転数の倍数に比例した一定周期で発生するホワールの軌跡は惑星の運動になぞらえて、“軌道”と呼ぶことがあります。
“ローター”は英語で“回転体”、“ダイナミクス”は英語で“動き”を意味する
つまり、大雑把に言えば“回転体の動き”そのものが“ローターダイナミクス”なんだ。
どのようなところで必要になるか
RDは高速回転する様々な機械を設計する時に使われます!例えば:
- 10万回転以上で回る工作機械のスピンドル
- 産業用のコンプレッサーやタービン
- 船舶のプロペラシャフト
- モーターや原動機全般
等など高速で回転する、あるいは大質量の軸が回転する機械ではほとんどと言って良い確率で登場します。
“回転体の振動”が一般的な振動と異なるのは、回転体は極めて大きな力学的エネルギーを持っているため、些細な振動でもトラブルになることが多く、綿密な検討が必要です。
RDの重要性
安定しないベイブレードをイメージした方はもうおわかりでしょう。ちゃんと回らないとすぐに止まってしまいます。回転機械においては、“回るか”、“回らないか”この二択しかありません。軸が暴れずにきちんと回る状態を専門用語では“Rotordynamic Stability (ローターダイナミクス安定性) “と呼びます。
いくら空力性能が良くても、軸受の摩擦が小さくても、RDが成立していなければ、そもそも機械としての機能を果たせなくなってしまうのです。最重要要素の一つですね!
軸振動とは
軸振動が発生する理由
わかったぜ!重心がずれてると振動するんだよな。ホイールバランスと同じで理解できたぞ!
たしかに不釣り合いは軸振動の発生する理由の一つです!
分かりやすい例として、”静的不釣り合い”と”偶的不釣り合い”を見てみましょう。

静的不釣り合い
これは完全にホイールバランスが狂っちゃって振動が出てる状態だな!
そうそう、ホイールに貼るこの重し。貼り方が悪かったり剥がれちゃうと嫌な振動が出て乗り心地が悪くなっちゃうよね。動画がこの静的不釣り合いが悪い状態のイメージです。
偶的不釣り合い
ん。。。これは、、
エンジンの振動か!?
正解!このように軸の上にいくつかの重量物があると、それぞれの重心ズレに応じて軸全体が複雑な振動をします。このような揺れ方を“偶的振動”と呼びます。
軸振動は軸そのものや軸受に大きな力を与えてしまうので、少ないほうが好ましいと言えます。仮に振動が出てもこのような小さな器具なら問題ありませんが、大型の産業機器などになると、大きな振動で機械自体が壊れてしまうのも想像できますね。
回転体の動きの種類
軸の動きは、大きく分けて、軸全体が動き回る”剛性”振動と、軸そのものが変形する”弾性”振動に分別できる。
あ~さっきのは”剛性”振動で他にもあるってことか
剛性振動
先程挙げた静的不釣り合いと偶的不釣り合いは軸そのものは変形しないので、共に剛性軸の振動の一種です。軸として最も単純な2点支持系で現ると、このような振動になります。先程の動画の動きをイメージしてみてください。
静不釣り合い

偶不釣り合い
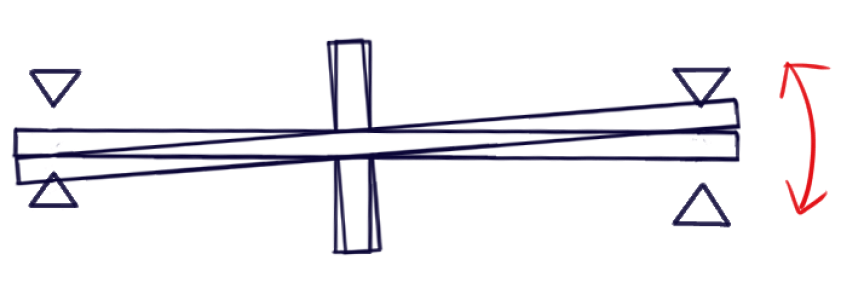
弾性振動
ある程度軸やローターが重くなったり、回転数が高くなると、軸自体が縄のように変形し始めます。これが弾性振動で、危険な振動の一種です。
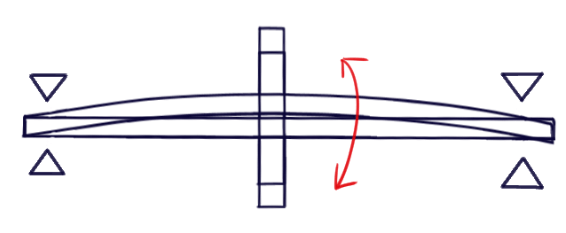
ねじれ方向振動
更に軸が長くなり、低速化すると、ねじれ方向の振動が出る場合があります。伝達トルクが大きい場合ねじれで破壊してしまうこともあり、数十mにも及ぶ船舶用のプロペラシャフト等が事例です。

軸振動による機械の破壊
軸振動が小さければ騒音程度で済みますが、振動が大きい場合は自分自身の回転エネルギーで機械内部の部品同士の接触、軸受の破壊、最悪の場合は軸の破断に繋がり、大きな被害をもたらします。
動画は旅客機用ターボファンエンジンのファンブレードが破断した場合を想定した破壊試験です。ファンは火薬を用いて破壊しますが、数枚欠けただけでエンジン全体が大きく変形し、非常に大きな振動が発生している様子が分かります。
バードストライク等でエンジンが破壊されるのは、ファンブレードの破片を吸い込むから、、というのももちろんですが、
結果的にはこのように軸受、軸、ケーシング自体にも大きな損傷を与えてしまい、こうなるともう修理不能です
最初から設計が悪いと、何もしていなくてもこのような動きをしてしまい、“回した瞬間に壊れる”ということもあり得ます。
バランシング
回転機械の振動の原因となる各要素の不釣り合いを減らす作業のことを“バランシング”を呼びます。バランスの取り方には主に二種類あり、双方共にあらゆる産業で広く利用されています。
静的バランス
軸が静止した状態で重心が軸の中心にくるように各部品の重量を調整します。最も分かりやすい例がタイヤ/ホイールのバランスウェイトの取り付けです。重心位置さえ分かれば簡単に実践できるため、回転するあらゆる機械で実施されます。
軸を回転して確認する場合、このように非常に低速回転でも十分に把握ができるため、低速バランシングとも呼ばれます。
動的バランス
軸全体に渡って各部品の重量を調整し、偶不釣り合いを無くす作業です。必ずしも静止した状態で軸の中心を重心が通るわけではなく、軸を回転しながら行う作業です。パランスを行う箇所によって、2面バランシング、多面バランシング、などいろいろな手法があります。
軸剛性が低かったり、ある程度高速回転する機械では必須の作業です。
このような超小型のターボチャージャーから巨大な軸流コンプレッサまで、基本的な作業内容は同じです。
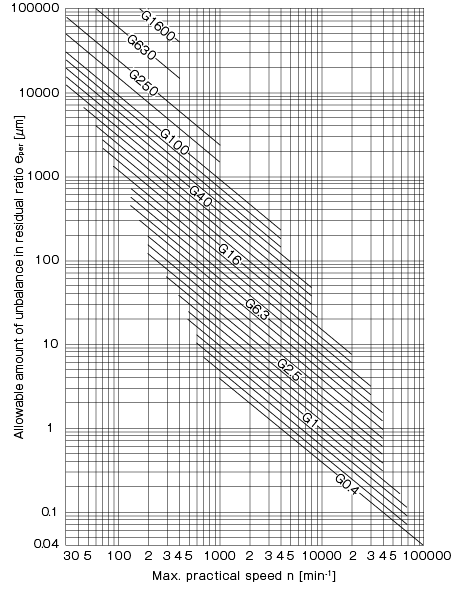
許容アンバランス
バランシングの最終目的は不釣り合いをゼロにすることではなく、軸受その他の耐久荷重未満となるよう、決められた許容値以下にすることです。
不釣り合いの残り量のことを残留不釣り合い等と呼び、mm・gの単位で表します。不釣り合いが同等の場合でも回転数によって深刻さが変わるため、回転数も考慮したバランススペックとしてISOバランスのG値も広く利用されます。G値は偏心量と回転数を対数表示として、バランスレベルを比率で表したものです。
精密機械では、1g質量が変わるとバランススペックに入らないこともありシビアな作業です。

















[…] 【ターボ機械シリーズ③】 ローターダイナミクスとは回転するあらゆる機械に影響するローターダイナミクス。どのような分野で、どうして重要なのかを説明します。… […]
[…] 考にしてみてください。・【ターボ機械シリーズ③】 ローターダイナミクスとは […]
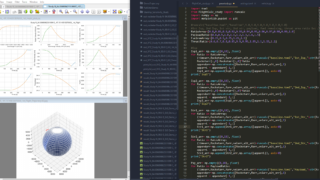
RD解析の自炊は勉強のために大変有効だと思います。2面バランサーを自作する際に参考させて頂きます!