回転体の振動
今までの話でなんとなくは分かったけど、ようは不釣り合いが小さければ起きないんじゃないのか?バランシングを頑張れば大丈夫に思うけど
うーん、バランスによって振動の大きさそのものは軽減するものの、本質的な対策にはならない場合が多いんだ。
不釣り合いが非常に小さい場合も大きな軸振動は起きちゃうことがあってキーワードは“支持剛性”と“軸剛性”だ。
軸支持部の変形
軸受、あるいは支持構造が変形するとはどういうことでしょう?ボールベアリングを例にみてみましょう。あらゆる軸受は、円滑な回転のために多少の隙間が設けられています。また軸受自体も金属等でてきているため、力を加えると変形します。この変形しにくさを“支持剛性”と呼びます。
ここではボールベアリングを事例として表していますが、そもそものバネ定数が小さく、減衰の大きい流体軸受や、応答遅れが発生する磁気軸受等では顕著に剛性の影響が現れるため、安定性を決定する上で第一に考えられるところです。
また、軸受に限らずシールなども軸に接触している以上、RD上は軸受として作用することがあり、考慮が必要になります。このような軸の要素すべてをまとめて軸支持部と表しています。
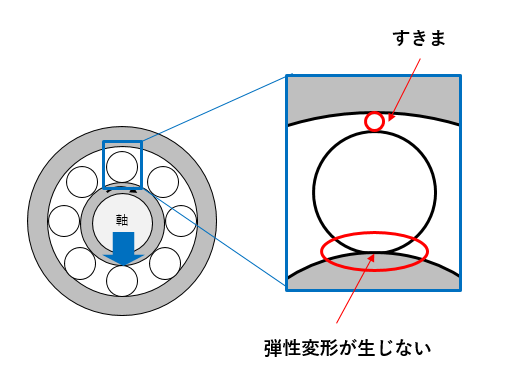
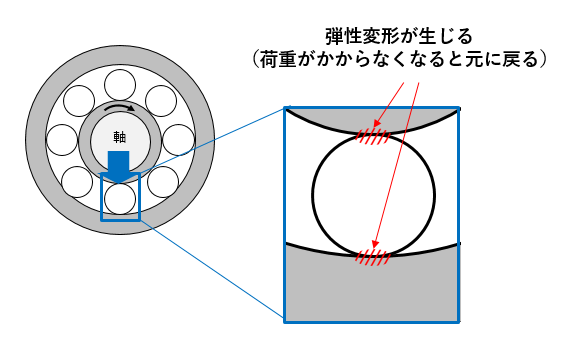
変形するということは、“バネとして作用する”ということです。バネがあるところには振動がありますよね。
したがって、軸受が存在する以上、必ず振動する領域が存在するのです。軸受は硬ければ良いと言うわけではなく、回転体によって安定して使える領域が決まっています。これらを探っていくのもRD解析の作業の一つです。
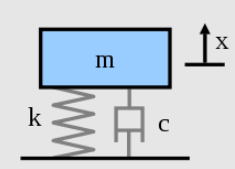
下の図のような系をイメージしてみてほしい。物理の授業で登場した、“バネ・マス・ダンパー系”だ。これと似たような状態に各軸受がなっていると思えば、想像しやすいだろう。
軸の変形
先程述べた通り、軸も変形します。軸の変形には様々なモードがあり、最も単純なものは図のように弓なりに変形するものです。この時の運動は軸の硬さ“軸剛性”と軸のモーメントによって決まります。軸の変形が安定している時は、軸全体が真ん中に重しをつけた縄跳びのような動きをします。
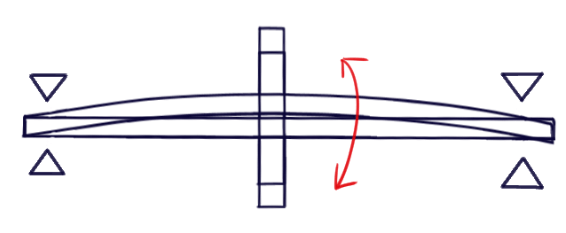
RD解析で難しいのは、軸が変形することによって軸受にかかる力が変わる→軸にかかる力が変わる→軸の変形が変化する といった具合に常に状態が変化する点だ。
一連の変形が回転の周期に合わせて一定な綺麗な運動となる場合、振動は安定している状態と言える。上図のような軸の変形を一周に渡って軌跡で表すと下図のようになるんだ。
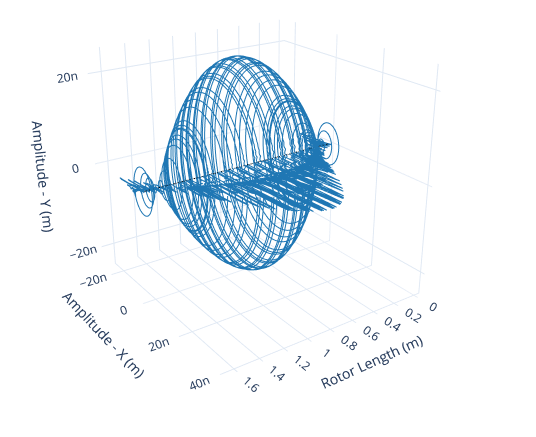
ジャイロ効果
周期的な触れ回りを発生させる主要要素はジャイロ効果です。歳差運動と同じ原理でおきるもので、仮に他の力をすべて無視した場合は軸の運動は安定した円形の軌跡を辿ることになります。
流体力の影響
ここまではただ回っているだけでも、軸は振動する、という点を説明しました。これに加え外力がかかると、軸の振動は助長されます。代表例としては、インペラやタービンに作用する流体力です。ローターに渡って不均一な力がかかることにより、周期的な外力として軸を不安定にさせる作用があります。

その他影響
上記以外にも加速度、外部振動、磁場やローター自体の変形によって軸に力がかかる場合、動きに影響を及ぼします。基本的にはすべて外力として作用し、用途によっては十分に考慮をする必要があります。
地上試験では問題なかったのに、いざ実機試験になると軸が暴れる、というモードもあります。
どのような使い方をすると危険性が潜んでいるのかを見極めるのもRD解析の重要な役割です。
剛性の種類と減衰
剛性の中身をもう少し細かくみると、”ばね定数:K”と“減衰定数:C”に分けることができます。また軸の上下方向と左右方向それぞれで定数が存在します。
- K: ばねとして左右する反力:例えば1kgfで押すと1mm縮む。下図ではばねに相当します。
- C: 速度に比例して決まる反力:回転数や周速に比例して反力が大きくなります。下図ではダンパーに相当します。

なんだか物理の授業で見たことがあるような気がしませんか??ここまできて段々とRDの正体が見えてきましたね。
固有値と危険回転数
そう、バネとダンパーがあるということは、軸系には固有値があるということです!
軸系の各要素のスペックが決まると、共振が起きる回転数が自ずと決まってきます。これを回転数の低い順に一次危険回転数、二次危険回転数。。。と呼びます。
共振が起きるとどうなるか、、、説明不要ですね!
共振が起きると、大きな振動が発生して、最悪機械の破壊に至る。
危険な共振がおきる回転数のことを危険回転数と呼ぶ。
とりあえずはこれだけを覚えておこう!
共振点が0Hzから数えて何個目のものかを1次、2字、、、という次数で表し、“モード”と呼びます。また各次での変形した形状を”モード形状”や“モードシェイプ”と呼びます。音波に例えると基本振動が一次モード、2倍振動が二次モード、それぞれの時の波の形がモードシェイプに対応します。
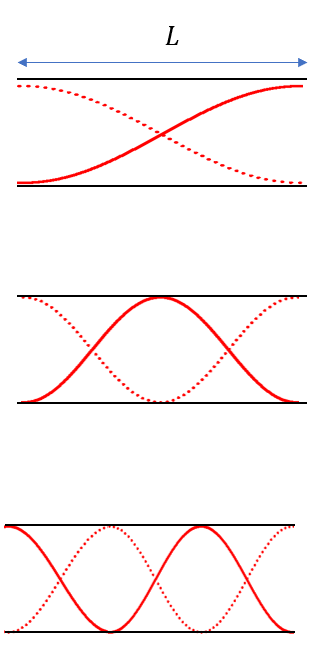
振れ回りの種類
ホワールには前向きと後ろ向きが存在します。それぞれ振れ回りが軸の回転方向に対して同じ向きか、反対方向かを表していて、発生する回転数も異なります。
軸の振動計測を行った際に得られる振幅だけでは、前回りなのか後ろ回りなのかが分からないため位相も確認する必要があります。また、どっち回りかによっても振動軽減に必要な対策も異なってきます。
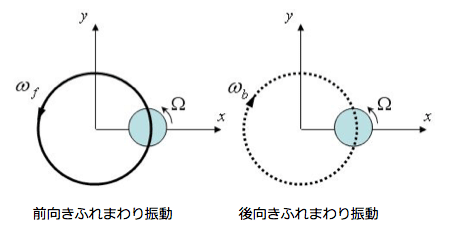
前回りを分かりやすく例えると、惑星の動きです。地球は自転しながら太陽の回りを回っていますが、この公転運動が前回りホワールに相当します。
後ろ回りというのは公転方向が逆転している状態なので一見不自然な感じがしますよね。しかし現実はどちらもよく発生し、また同じ回転数でも軸受け毎に異なることが多々あります。
(軸受1では前回りだけど軸受2では後ろ回り)
こうなると軸は非常に複雑な動きをすることが想像できますね。
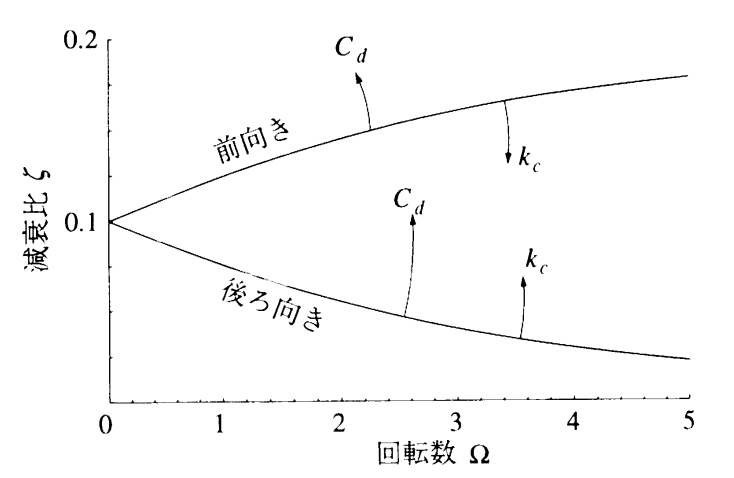
軸の安定化のためにKやCを変更した際の影響を表したものが上図です。減衰は高いに越したことはありませんが、支持剛性が高ければ良いというわけではないことが分かります。
軸の設計って難しいんだなぁ、ただ単にバランスを取ればいいだけだと思ってたぜ
でもひとつ勉強になったね。複素数なんて日常生活のどこで、、って今度誰かに言われたら回転機械と近代文明には100%必須だよ!って言う事ができます!勉強だいじ!
次のページはいよいよ本題、軸振動と対策についてです。

















[…] 【ターボ機械シリーズ③】 ローターダイナミクスとは回転するあらゆる機械に影響するローターダイナミクス。どのような分野で、どうして重要なのかを説明します。… […]