はじめに
早速質問です。ガスタービンの出力ってどうやって決まるか分かりますか？
そうだなぁ、コンプレッサーの直径とか回転数？どれだけたくさん回せるか、かな？後はコンプレッサとかタービンそれぞれの効率とか。
後はそうだ、タービン入口温度が重要だって聞いたよ。年々上がってるんだってね。
簡単！どれだけたくさん燃料を燃やせるか？じゃない？
全員(ほぼ)正解ですね！？本日はガスタービンの動作の基本となる、タービンパワーマッチングについて見ていきましょう。ターボコンプレッサーやガスタービンはじめ、多くのターボ機械で必ず登場する考え方なので、ここを抑えておくと色々と便利です。
- 専門外だけど、ガスタービンの出力や定格点がどのように決まるか興味がある。
- 熱力学の授業でブレイトンサイクルを習ったけど、いまいちピンと来なかった。より具体的な使用例を見てみたい。
- 新聞や産業関係のニュースで”タービン入口温度1700℃”のような記事を見た時に、それの意味するところを理解できるようになりたい。
- ラジコン用のジェットエンジンやチューニングカーのタービン選定をしたい。
- 今回の記事のレーティング：
熱力学のおさらい
ブレイトンサイクルのおさらい
最初にブレイトンサイクルのおさらいです。4つの過程から成りますが、実際には4→1は排気と吸気に該当するため、開放型ブレイトンサイクルであるガスタービンにおいては、あまり意識しません。(推力と排熱として考えてしまって良いです。)
- 1→2：軸動力を使ってコンプレッサが仕事をする過程。断熱圧縮。
- 2→3：燃料を燃焼させる過程。等圧加熱
- 3→4：膨張仕事をタービンに与える過程。断熱膨張。
実際にはコンプレッサ、タービンの効率は100%ではないので、損失分だけ図の赤線ようにずれます。圧縮過程と膨張過程で失われたエンタルピΔhは最終的に利用できる出力から失われるため、図のような等式が成り立ちます。また、コンプレッサ動力はタービン動力 – 損失に等しいため、コンプレッサ動力以上に投入された過剰なエネルギーは排気ガスとして捨てられるか、パワータービン等で回収されることになります。
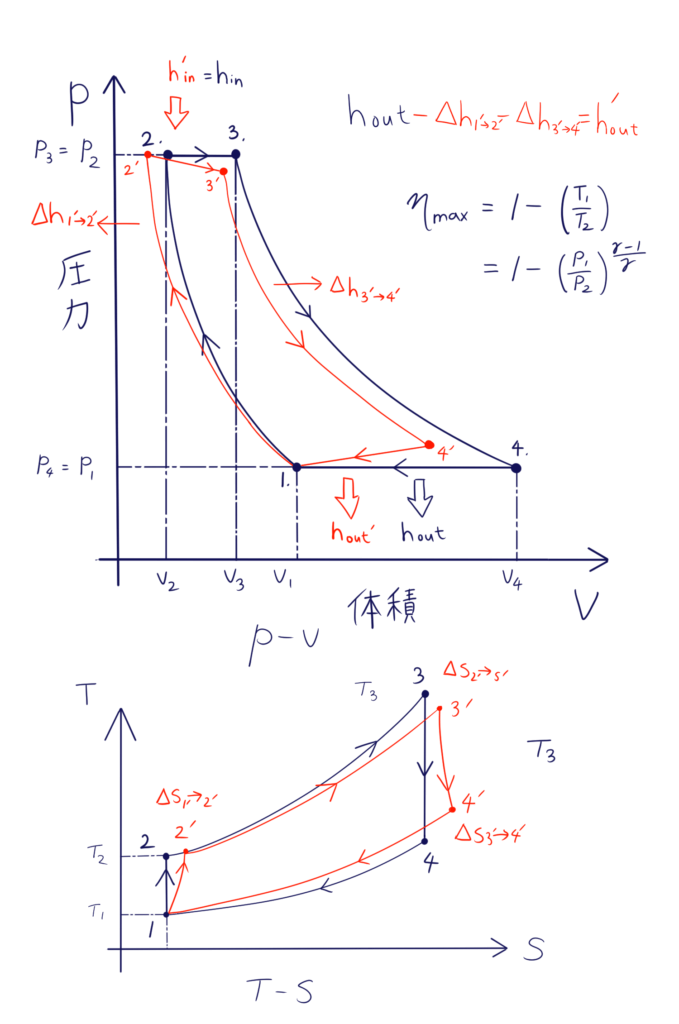
\( \gamma: 比熱比 \)
なつかし～～ あったね、こういうの。私オットーサイクル、ディーゼルサイクル、ランキンサイクルってやつだね。
ほとんどの熱サイクルはそうですが、ブレイトンサイクルも圧力比が高いほど熱効率が優れる、ということがよく分かりますね。
ガスタービンの簡略化モデル
ターボ機械シリーズ第一回では代表的なターボ機械やガスタービンエンジンの簡単な構造について説明しました。実際のエンジンでは様々な細かい部品があり、すべての影響を完全に見積もるのは非常に大変です。そのため、企画や初期設計の段階では、しばしば簡略化したシステムで考えるのが主流です。特にガスタービンの性能へ影響を及ぼすものとして下記があります：
- Compressor Overall Pressure Ratio (OPR) PRC：コンプレッサの全段圧力比。すべてのコンプレッサ段の合計圧力比。
- Turbine Overall Pressure Ratio (OPR) PRT: タービンの全段圧力比。すべてのタービン段の合計圧力比。
- Compressor Adiabatic Efficiency (ηc): コンプレッサ断熱効率：コンプレッサのエントロピー増加を示す効率。 効率100%の場合完全断熱過程とみなせる。
- Turbine Adiabatic Efficiency (ηT):タービン断熱効率。
- Combustor:燃焼器。燃料を空気と混ぜて燃やす装置。本当の役割はたった一つで、タービン上流にエンタルピーを投入することです。
- Cp [kJ/kgK]: 定圧比熱。温度や組成によって異なるため、コンプレッサ段、タービン段それぞれで違う値を使用する。
- γ [-]：比熱比。Cp/Cv。温度や組成によって異なる。標準乾燥空気では 約1.395。
- HHV [MJ/kg] (Higher Heating Value) ：燃料熱価。1kgの燃料を完全燃焼させた時に発生するエネルギー。本記事では一般的な灯油や軽油を想定し、46.2[MJ/kg]と仮定します。
- Standard Atmosphere: 標準大気。ガスタービンの効率は気圧や気温の影響を受けます。これを補正するために、静止標準大気 (Sea Level Static) を用います。 T=15[℃]、P=101.325[kPa]に相当。
- 質量流量 W [kg/s]：体積流量 Q [m3/s] X 密度ρ [kg/m3] のこと。密度によって変わる。ターボ機械では体積流量で計算を行うことが多いため、変換することが多い。
- Wf [kg/s]: 燃料流量。
- Wa [kg/s]: 圧縮機吸い込み空気流量。圧縮する空気の量に等しい。
- Wc [kg/s]: 燃焼空気流量。圧縮した空気のうち、燃焼器に送られる量。一部は抽気として、捨てられる。
- Wt [kg/s]：タービン流入空気量。燃焼ガスは通常は全量がタービンに送られるが、ブリード方式やバイパス方式など、一部をタービンに流入させない設計のものもある。(今回は簡素化のため全量を使います。)
- Wb [kg/s]：抽気量。圧縮された空気の一部はタービン翼の冷却や補助動力、与圧等のために一部の空気は燃焼器へは送られず、バイパスされる。実質的には利用されない空気分圧縮仕事はロスになるので、損失として扱う。
- H1c = H1 [kW]：コンプレッサ流入エンタルピ。最初から吸込み空気が有している圧力、流速など。静止状態では排気側も同じ条件のため、ゼロとして扱う。
- H2c = H2 [kW]：コンプレッサ流出エンタルピ。圧縮仕事を与えられた空気。
- Hb [kW]：抽気損失エンタルピ。Wbと共に失われるエネルギー
- ΔHf [kW]：燃焼器発生熱量。燃料流量 x 発熱量
- H1t = H3[kW]：タービン流入エンタルピ。タービンを回すエネルギー源、つまり燃焼ガスの持つエンタルピ。
- H2t = H4 [kW]：タービン流出エンタルピ。タービンではすべてのエネルギーは回収できず、一部はWoutと共に流出する。流出分は、後段のパワータービンの駆動や、ノズルによって推力に変換される。
- Pw [kW] :軸動力。タービンで回収したエネルギーをコンプレッサに伝える。Ht – 損失 に等しい。
- H_loss [kW]：軸受損失。軸受以外にも補機類の駆動動力や各種抵抗、圧損等諸々を含んだ軸動力から奪われる動力。
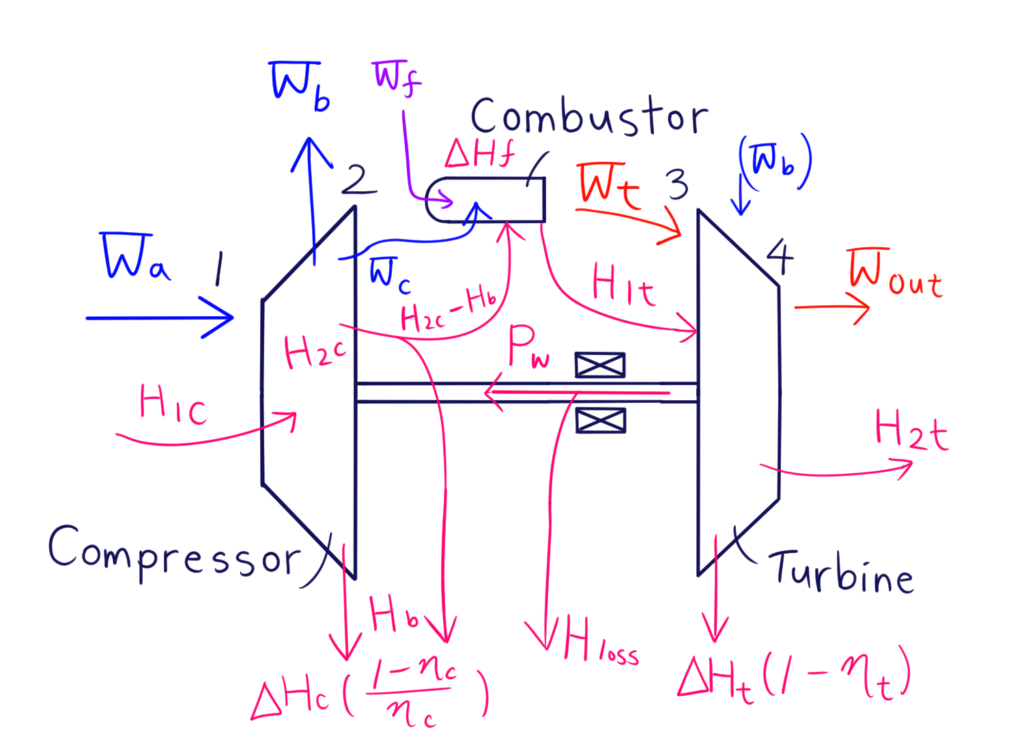
模式図ではブレイトンサイクルの図の各過程1~4に対応しています。それぞれW、Hで質量の流れとエネルギーの流れを表しています。
青線がコンプレッサに出入りする質量、赤色がタービンに出入りする質量、ピンク色がエネルギーの授受かな。質量保存の法則、エネルギー保存の法則だね。紫は燃料ってことかな。模式図にするとこんな感じだね。
ここまではなんとなく覚えてる方も多いと思います。ただ授業でこれだけ説明されても、あまり具体的なイメージが沸きにくいし、何より“つまらない”というのがあるかなと思います。
ただただ公式を習うだけじゃなくて、実際にそれを応用して、はじめて楽しさがあると思っています。一歩ずつ説明するので一緒に見ていきましょう!
支配方程式
前章で作った模式図を元にガスタービンの各部分の熱力学的変化を見ていきましょう。熱力学の断熱圧縮の式を用います。
等圧過程のエネルギー授受
② \( \Delta h = C_p \Delta T \)
コンプレッサ出口温度：入口温度と出口温度の関係
③ \( T_2 = T_{2c} = T_{1c} \frac{1}{\eta_C} (PRC^\frac{\gamma – 1}{\gamma} – 1) +T_{1c} \)
コンプレッサ圧縮仕事： 空気の圧縮に必要な仕事
④ \( \Delta h_c = h_{2c} – h_{1c} = \frac{1}{\eta_c} Cp_c T_{1c} (PRC^\frac{\gamma – 1}{\gamma} -1) \)
タービン出口温度：入口温度と出口温度の関係
⑤ \( T_4 = T_{2t} = T_{1t} (PRT^\frac{\gamma – 1}{\gamma} – 1) \eta_t + T_{1t} \)
タービン膨張仕事：タービンから取り出せる膨張仕事
⑥ \( \Delta h_t = h_{1t} – h_{2t} = \eta_t Cp_t T_{1t} (1- PRT^\frac{\gamma – 1}{\gamma}) \)
次に質量のバランスを見てみましょう。質量保存の法則から、系に流入する質量と流出する質量は定常運転をしている時は一定です。ターボファンエンジンなどは冷却抽気以外に空気流れがあり、また様々なバイパス経路が存在しますが、ここでは丸めて損失として取り扱い、流出はないものとして考えます。
コンプレッサー流量及び抽気
⑦ \( W_a = W_c + W_b \)
燃焼器流量
⑧ \( W_c + W_f = W_t \)
タービン流量及び冷却空気
⑨ \( W_t + W_b = W_{out} \)
質量流量と体積流量の関係 (すべてに適用)
⑩ \( W = \rho Q \)
最後にエネルギーバランスです。軸動力Pwがコンプレッサ動力ΔHcと等しい時、軸は一定の回転数で周り、平衡が保たれます。エネルギーと質量のバランスが成立している時、簡素化モデルは0次元の系になります。
燃焼ガスの温度
温度効率をηcbと仮定すると：
⑪ \( H_f = HHV * W_f * \eta_{cb} \)
タービン入口温度：
⑫ \( T_{1t} = T_{2c} + \frac{H_f}{Cp_2 W_t} \)
排気エンタルピ Hout
⑬ \( H_{out} = H_f + H_c – H_{loss} – H_t \)
ここから分かる通り、燃焼器での投入エンタルピHfがガスタービンの動力源となり、使用されなかった残りはすべて排気に捨てられます。残りの不明変数はコンプレッサ・タービンそれぞれの効率、また回転数と圧力比、流量の関係です。これらは概算することも可能ですが、一般的には”マップ”を用いて、計算を行います。取得方法について、次の章で見てみましょう。
忘れた人、初見の人は心配しなくても大丈夫です。今回は実用的なお話なので、公式を使えば誰でも計算ができます。どうしても公式の導出をしたい人、深く知りたい人には最後に参考文献を書いてあるので、熱力学の教科書を読んでみてくださいね。
コンプレッサー・タービンマップ
実在流体では比熱比γに沿った断熱変化ではなく、任意のポリトロープ指数nに置き換えられますが、nの値を知ることは難しいため、多くの場合では代わりにコンプレッサ効率ηc、タービン効率ηtを経験式や過去の実績から仮定して計算を行います。
厄介なのは、ηc、ηtは同じ形状のコンプレッサやタービンでも、体積流量と圧力比によって変化することです。これを表したのが、予め性能予測や実機試験から得られたデータです。圧力と流量の関係を表すことから、P-Q曲線、P-Q特性などと呼ばれることもあります。
- Compressor Map：コンプレッサーマップ：ηc、Nc = f (PRC、Qc)
- Turbine Map：タービンマップ：ηt、Nt = f(PRT、Qt)
コンプレッサ、タービンマップについてはまた別の機会に詳細の記事を書く予定です。今知ってほしいのは、とあるコンプレッサの圧力比 (PRC)と体積流量 Qc が決まったら、マップから勝手に回転数N と効率η が得られることです。タービン側はもっと簡単で、タービンノズルでチョークしているため、ほぼほぼ体積流量が一定になります。
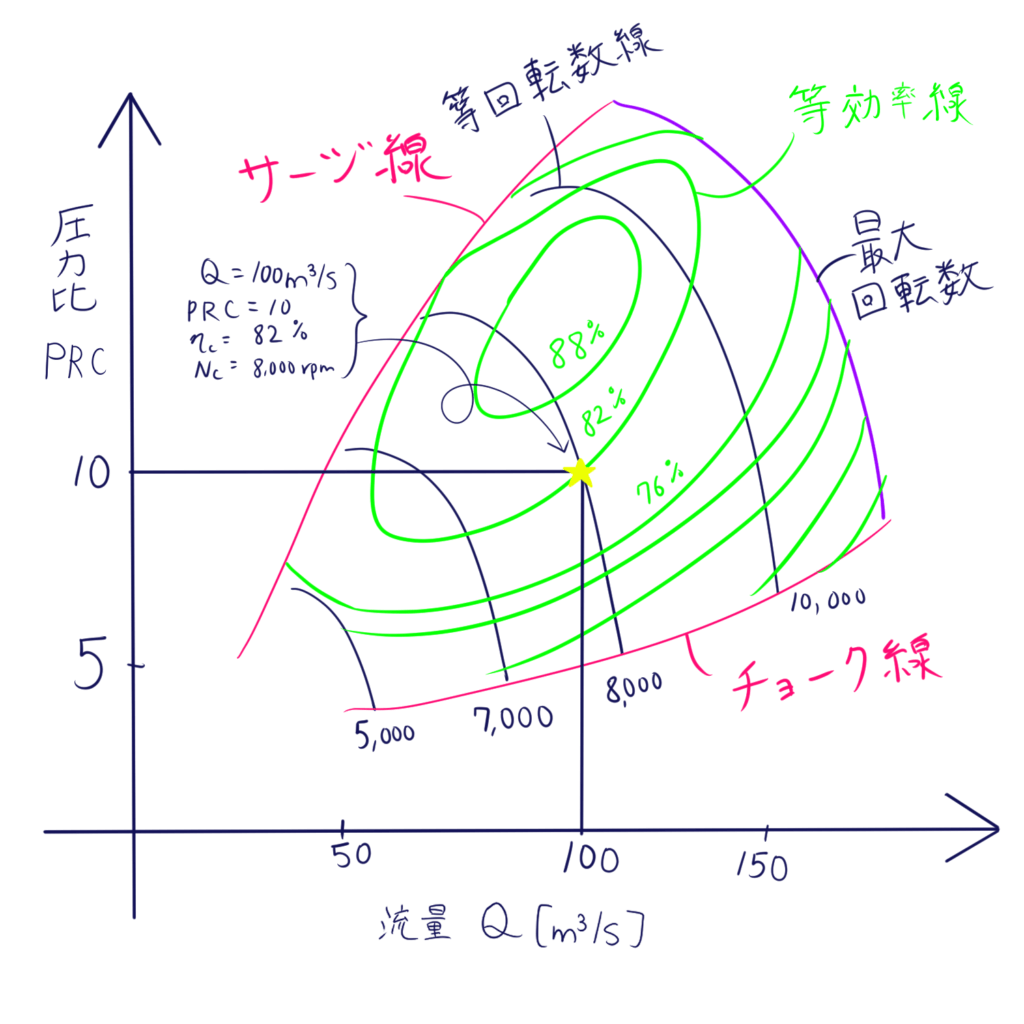
これらのマップは標準大気での体積流量を元に作成されているため、異なる温度、圧力条件で使用する場合は、補正が必要となります。補正後の流量と回転数をそれぞれ、“修正流量”、”修正回転数”と呼び、マップを読み取る際に変換が必要です。
修正流量
⑭ \( Q* = Q \frac{101.325}{P} \sqrt{\frac{T}{288.15}} \)
修正回転数
⑮ \( N* = N \sqrt{\frac{288.15}{T}} \)
また全く同一形状で大きさや回転数の異なるのコンプレッサでは、下記の式より性能を概算することも可能です。これを“相似則”と呼びます。しかし現実には空力的に理想的な効率を発揮できる回転数は1点しかないため、ズレが発生します。
状態1.と2.の相似： 流量
⑯ \( \frac{Q2}{Q1} = \frac{N2}{N1} \)
ヘッド(圧力)
⑰ \( \frac{P2}{P1} = (\frac{N2}{N1})^2 \)
パワー
⑱ \( \frac{Pw2}{Pw1} = \frac{P_2 Q_2}{P_1 Q_1} = (\frac{N2}{N1})^3 \)
計算手順
計算手順
1軸ターボジェットとして、また各段はコンプレッサ段1段、タービン段1段として簡素化して考えてパワーマッチングを行ってみましょう。大まかな計算手順は下記の通りです：
- 狙いの吸込み流量を決める=>コンプレッサ入口流量Qcとして代入。
- 回転数を仮定する：マップを観ながらQcが近いところの回転数Nc、圧力比PRCを選択。
- 選択したPRCでコンプレッサ出口圧力P2c、コンプレッサ必要仕事Hcを計算する。
- Wc、Wb、Wfそれぞれからタービン流入質量を求め、またタービン入口温度圧力T1t,P1tを求める。
- タービン圧力比と温度から、タービン動力を計算する。回転数は軸で接続されているため、コンプレッサーと同等と仮定する。なお、タービンマップで上ではほとんどの場合チョーク領域で運転するため、圧力比を変えても密度=質量流量のみが変化し、体積流量はほぼ一定になる。出口圧力一定であればPRTはP1tに反比例すると見なせる。
- タービン動力から損失を差し引き、コンプレッサーに伝わる軸動力を求める。
- 軸動力とコンプレッサ動力のバランスを確認する。タービン動力が上回っている場合、定格点=マッチポイント、はより高い回転数に、下回る場合は低い回転数にある。エネルギーが余っている状態だと更に回転する、とイメージしていただければよいかと思います。
- 上記を軸動力とコンプレッサ動力が一致するまで繰り返す。
- この時の回転数、圧力比、流量が定格運転点になる。
コンプレッサー動力の計算
- PRCを仮定したので、式③、式④からコンプレッサ出口温度T2cとコンプレッサ動力Hcを計算する。
- タービン入口条件を決めるために、式⑦、式⑧からタービン入口流量Wt、式⑫からタービン入口温度T1tを計算する。
タービン動力の計算
- 仮定したタービン出口圧力P2cよりタービン圧力比PRTを求める。
- PRT、式⑤、式⑥よりタービン出口温度T2t、タービン仕事Htを計算する。
- Htと損失Hlossより軸出力Pwを計算する。Pw=Ht-Hloss。
余剰パワーの精算
- Pw/Hcが軸出力とコンプレッサ動力の比になる。軸出力が上回っている場合は、より大きなコンプレッサ動力が発生され、つまり回転数が上昇する。
一回目の計算では、適用に回転数を決めているため、タービンパワーとコンプレッサパワーが一致しておらず、また回転数も異なる状態と思います。従って必ず平衡を保つために回転数が変化するはずです。平衡状態では軸出力とコンプレッサ動力が=の状態のはずなので、そうなるまで回転数を操作する作業になります。
演習
さて、前章で示した計算手順に沿って、架空のターボジェットエンジンの動力を計算してみましょう！勉強も兼ねて、初めてやる時は手計算でやることをおすすめします。(作業ゲーなので、一度理解したら今後はソルバーなどを使って楽をしてください。)
環境変数・仕様の設定
計算のため、下記のような条件を仮定してみましょう。前章でも述べた通り、実際にはコンプレッサ、タービンは回転数や圧力比で効率が変化しますが、今回は簡素化のため、”固定”として考えます。また、理想的な特性をもつため、P-Q特性は相似則に基づくものとしましょう。
実際に効率一定の翼車を開発することができたら、もうそれは革命です。一般的には圧力比が何割かも変わると効率は激変します。
今回は手計算でやる、ということに主眼を置いて、効率は一定でやってみましょう。
環境変数
| コンプレッサ入口比熱、比熱比 Cp1 [kJ/kgK],[-] | 1.004, 1.4 |
| コンプレッサ入口密度 ρ1 [kg/m3] | 1.225 |
| コンプレッサ入口温度圧力：P1、T1 (吸込み温度圧力) [kPa],[K] | 101.325, 298.15 |
| タービン入口比熱、比熱比 Cp3 [kJ/kgK],[-] | 1.2, 1.35 |
| AFR, 温度効率 | 60, 85% |
| 燃料発熱量HHV [MJ/kgK] | 46.2 |
| タービン出口圧力、吸込み大気圧力比 P2t/P1c | 105% |
| 抽気ブリード比 Wb/Wc | 20% |
| 軸受損失 Hloss/Ht | 10% |
| 燃焼器圧損 (P2c – P1t 燃焼器で失われる圧力) | 5% |
| 燃焼器平均比熱 Cp2 [kJ/kgK] | 1.1 |
タービン出口圧力は理想的には吸込み圧と同等ですが、実際にはノズル損失などがあり、やや高めになってしまいます。
今回はあくまでパワーマッチングの目的のため、既知の値を用いて観ていきましょう。
初期値の仮定
次に計算を始めるために仮に初期値を設定してみましょう。これらの値はあくまで初期値で計算をしながら逐次更新されます。
計算初期値
| コンプレッサ回転数 NC = N1 = NT [rpm] | 30,000 |
| コンプレッサ圧力比 PRC [-] | 5 |
| コンプレッサ入口流量 Wc [m3/s] | 5 |
| コンプレッサ効率 ηc (一定と仮定) @ 30,000 [rpm] | 0.8 |
| タービン効率 ηt (一定と仮定) @ 30,000 [rpm] | 0.8 |
今回使うマップ
計算用にもしこんなマップがあったら、というのを仮定してみましょう。
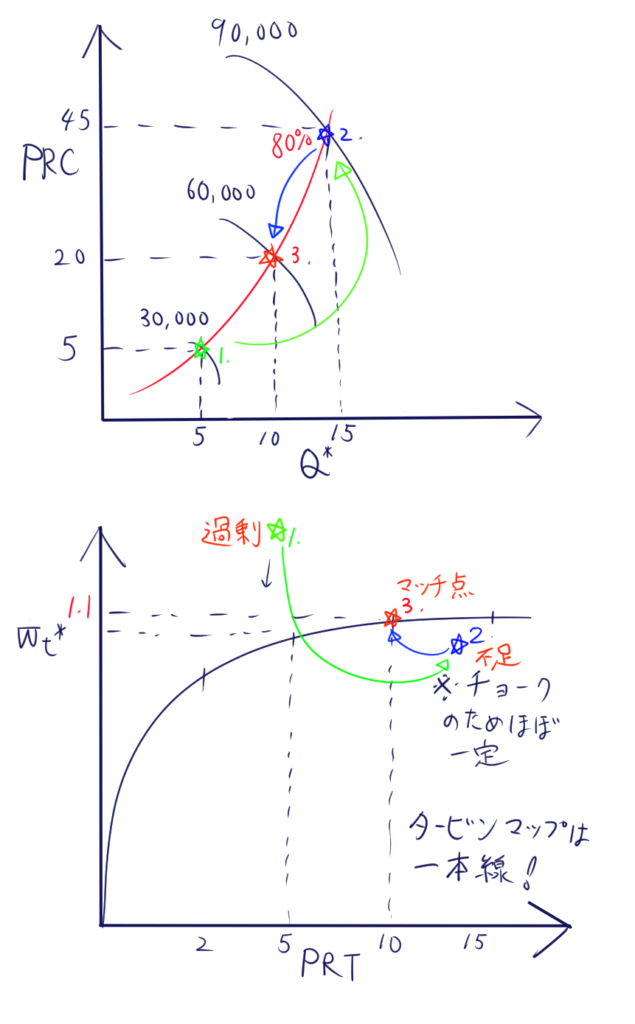
計算条件が揃いました！支配方程式を使って一緒に解いてみましょう。
計算一回目
①：コンプレッサ吐出条件と必要動力
| コンプレッサ回転数、圧力比、流量 Nc. PRC, Qc | 30,000[rpm], 5.0, 5.0 [m3/s] |
| コンプレッサ出口温度 T2c | 242 [degC] |
| コンプレッサ仕事 Hc (圧縮仕事/ηc) | 1338 [kW] |
②：燃焼器とタービン入口条件
| 燃料発生熱量 Hf | 3207 [kW] | |
| 燃焼器空気質量Wcb、抽気質量流量Wb | 4.9 [kg/s], 1.2 [kg/s] | |
| タービン質量流量Wt | 4.98 [kg/s] | |
| タービン入口温度 T1t | 827 [degC] | |
| タービン入口圧力 P1t | 481 [kPa] |
③：タービン出口条件とタービン動力
| タービン出口温度 T2t | 542 [degC] |
| タービン出口圧力 P2t | 106.4 [kPa] |
| タービン仕事 Ht | 1705 [kW] |
④：損失の計算
| 軸損失 Hloss | 171 [kW] |
| 軸出力 Pw | 1535 [kW] |
| 排気エンタルピ Hout | 1708 [kW] |
| 抽気損失エンタルピ Hb | 267 [kW] |
⑤：パワー差
| 軸出力/コンプレッサ動力比 Pw/Hc | 1535/1338 = 1.15 |
| 軸出力/燃料発生熱量 Hf | 1535/3207 = 0.47 |
| 判定： | 実回転数 (コンプレッサ動力) > 推定回転数 |
軸出力が高すぎ、成立しないね。。。
この状態だと、回転数が上昇してコンプレッサ動力がもっと大きくなるはずです。コンプレッサ、タービンマップ上では1.の状態です。それでは二回目は90,000rpmと仮定して再計算してみましょう。
計算二回目
コンプレッサ吐出条件と必要動力
| コンプレッサ回転数、圧力比、流量 Nc. PRC, Qc | 90,000 [rpm], 45, 15[m3/s] |
| コンプレッサ出口温度 T2c | 758 [degC] |
| コンプレッサ仕事 Hc (圧縮仕事/ηc) | 13525 [kW] |
なんと回転数を90,000rpmにすると一気にコンプレッサ入口温度とコンプレッサ動力が上がってしまいました。一回目の計算と同様にパワーバランスを計算してみましょう。
二回目結果
| タービン入口温度 T1t | 1343 [degC] |
| タービン出口温度 T2t | 544 [degC] |
| タービン動力 Ht | 14321 [kW] |
| 軸出力 Pw | 12889 [kW] |
| 軸出力/コンプレッサー動力 | 0.95 |
今度は高すぎた。うーん、これ何回やったらいいんだろ
タービンパワーが足りないので、もっと低いところでマッチングするはずです。もうちょっと下げてみましょう。
収束計算
上記のように回転数を変えながら、Pw = Hc のバランスが成立するまで探ります。
~6時間後~
もう無理だよ～ 何回やっても合わない！せめてパソコンで計算させてよ！
あ、釣れたよ～！(あつ森プレイ中)
て、かずおまだやってたの？私面倒くさくなっちゃってプログラムで解いちゃったよ
放置しててごめんね。30分ぐらいで飽きて何か言ってくると思ってて、、、^^;
NC = 66300 rpm にしてみましょう。
コンプレッサ吐出条件と必要動力
| コンプレッサ回転数、圧力比、流量 Nc. PRC, Qc | 66,300 [rpm] 24.4, 11.1 [m3/s] |
| コンプレッサ出口温度 T2c | 580 [degC] |
| コンプレッサ仕事 Hc (圧縮仕事/ηc) | 7555 [kW] |
収束計算結果
| タービン入口温度 T1t | 1166 [degC] |
| タービン出口温度 T2t | 531 [degC] |
| タービン動力 Ht | 8394 [kW] |
| 軸出力 Pw | 7555 [kW] |
| 軸出力/コンプレッサー動力 | 1 |
ついに解けました！ついに6万6300回転で平衡しましたね。この時の軸出力はなんと1万1000馬力を発生しています。しかしこのガスタービンにはひとつ悲しいことがあります。
計算の前提で置いた通り、タービン出口圧力はほぼ大気圧、軸出力はすべてコンプレッサーを駆動するのに使われています。つまりこのエンジンから取り出せる軸出力、あるいは推力はほとんどありません。
１万馬力も発生しているのに、回転してるだけで精一杯だなんて、、、
やっぱりただ回るだけのガスタービンとちゃんと動力源として使えるガスタービンとじゃ難易度も違いそうだね
やってみてわかったけど、ガスタービンてそもそもコンプレッサの動力が大部分だから、コンプレッサやタービンの効率が1%変わると取り出せる動力が全く変わってしまう、すごくシビアな世界だよね。。。
タービン動力と損失、コンプレッサ必要動力が釣り合った状態では、回転数は一定となり、安定した定常運転状態になります。この回転数を“マッチング回転数”と呼ぶことがあります。動力を目的関数とすることで、非常に簡潔に解くことができるので、最も便利な簡易計算方法です。
このような繰り返し計算はプログラム上で実施するのが効率的かつ当たり前です。しかし、かつて上記の作業を印刷されたマップから読み取り、計算尺で逐次設計していた時代がありました。莫大な作業量ですよね、昔の偉人たちには頭が上がりません。。。
コンピューター (計算士)という専門の職業の人が朝から晩までゴリゴリと計算していた時代もあったのよ。。。21世紀は便利な時代になったわ。
実際のターボ機械への適用
多段の場合
コンプレッサやタービンが多段ある場合、それぞれの段で昇圧を考える必要があります。複数の段数の合計の昇圧を“OPR (Overall Pressure Ratio)”と呼び、これを使って前章のような簡易解析を行うのが一般的です。
ｎ段 の場合の圧縮比
⑲ \( OPR = \prod_{k=1}^{n} PRC = PRC_1 * PRC_2 …. * PRC_n \)
ｎ段 の場合のパワー
⑳ \( P_{Total} = \sum_{k=1}^{n} P_k = P_1 + P_2 + … + P_n \)
便利なことに、段数が多くても、全体の積=OPRと仕事量の和はほぼ一定になります。現実には単段の圧力比が小さい方が効率を稼ぎやすく、全体効率が向上する傾向にあるため、ガスタービンでは多段軸流コンプレッサがよく使われます。一方で段数が増えるほど運転範囲が狭くなり、運転のフレキシビリティが失われるため、負荷変動が大きな用途にはあまり向きません。
段数がたくさんあってもOPRで考える。
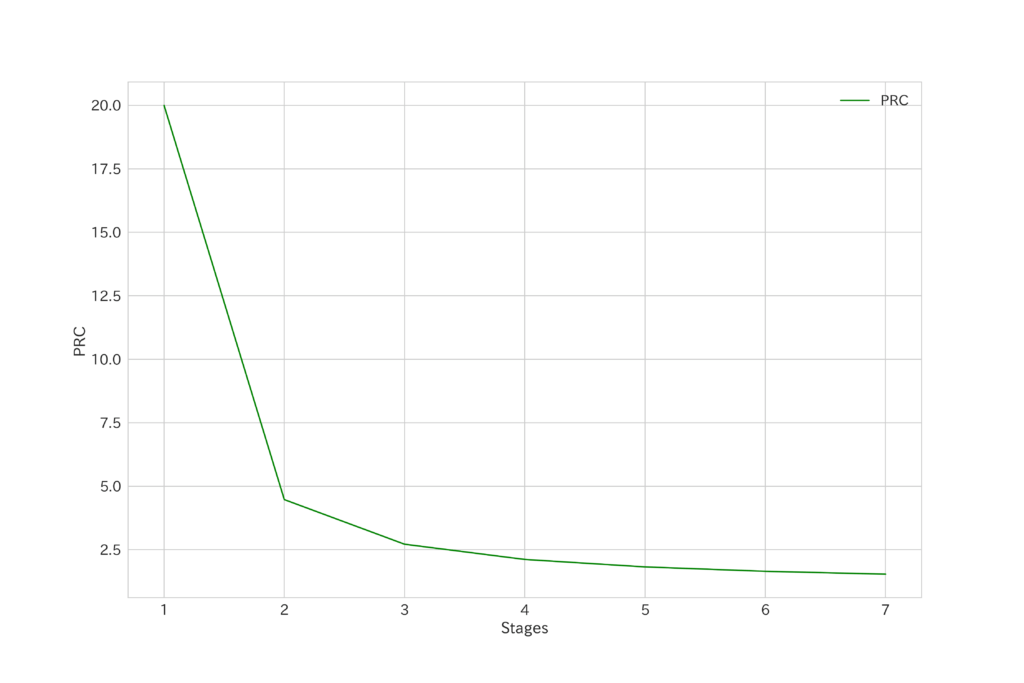
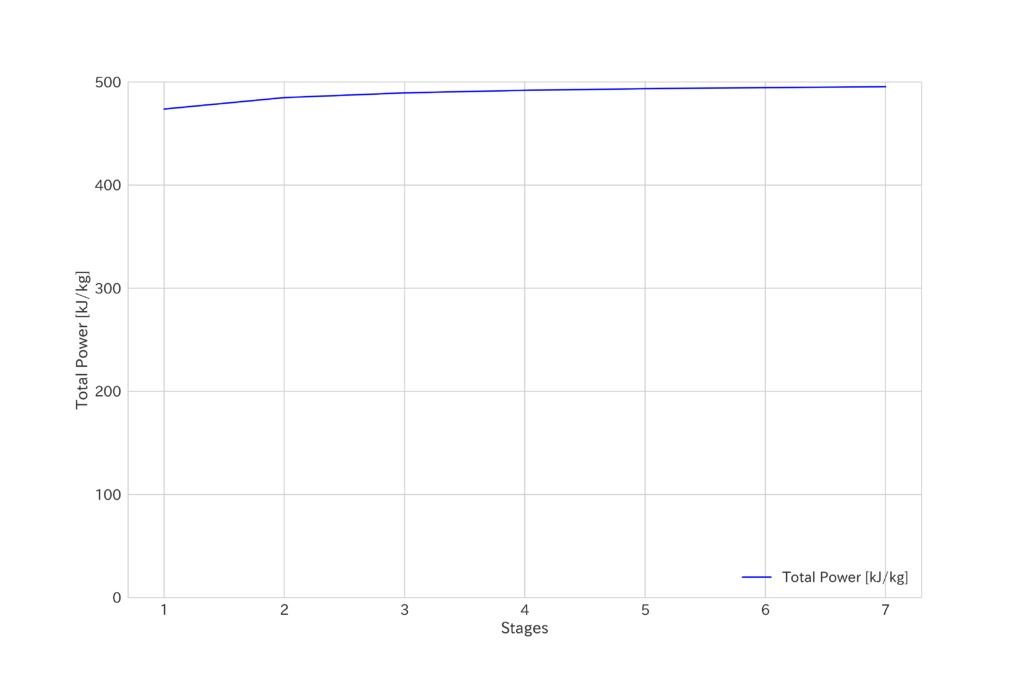
前章で述べたOPRについて、段数が変わってもOPRが同一であれば、基本的には仕事量は変わりません。計算で差が出るのは、温度によって定圧比熱Cpが若干変化するためです。数百Kのオーダーであれば、誤差は数%なのでほぼ一定と見なせます。下図はOPR=20とした時に段数を変えた場合の各段あたりの圧力比と合計仕事量です。
軸動力を取り出す場合
ガスタービンから軸出力を取り出す方法は2つあります。
直動方式
コンプレッサ駆動軸に直接ギアボックスなどを取り付けて出力を取り出す方法。C130等で使われるベストセラーであるAllison T-56はこの方式です。コンプレッサ駆動軸は回転数が非常に高いため、ギアボックスが大型化しやすく、また効率に劣るなどのデメリットもありますが、構造が簡素化できるのが強みです。
この方式の場合、前章で軸受損失として設定していたHlossにほしい動力を加えてやるだけで、あたかも軸から得られる動力がタービン側から観ると損失のように取り扱うことができます。この場合マッチングは前章の演習と同じように行えば、軸出力が得られます。
軸出力
\( Pw = H_t – H_{loss} – H_c \)
パワータービン方式
コンプレッサ駆動タービンの後流に軸動力回収専用にもう一段タービンを追加する方法。大多数のターボプロップやターボシャフトエンジンはこの方式です。しかしタービンの段数が増えるため、OPRを増やすか、コンプレッサ駆動タービンの圧力比を下げるしか出力を得る方法がないので、高効率なタービンや高い圧縮比と高性能な燃焼器が必要になってきます。
タービン膨張仕事：タービンから取り出せる膨張仕事
\( \Delta H_t = \eta_t Cp_t T_{1t} (1- PRT^\frac{\gamma – 1}{\gamma}) \)
ただし \( PRT_1 * PRT_2 = OPR \)
前章の計算から、30,000rpmでは余剰動力は15%ほどしかありませんでした。つまり効率80%程度のコンプレッサ、タービンだとほとんどの動力はコンプレッサを駆動するためだけに使われてしまい軸出力に使えるのは極一部しかないということになります。
また、マッチングポイントであった66,300rpmでは余剰動力はゼロのため、負荷が存在しない場合の最高回転数とも見なせます。
ブレイトンサイクルはガソリンエンジンなどで使われるオットーサイクルと比較すると熱効率に劣り、高い圧縮比とより高効率な設計をしないと燃費が悪化してしまうということが如実に現れています。
ファンを駆動する場合
ターボファンエンジンではコンプレッサの前段にファンが存在するため、コンプレッサ吸込みの段階で既に圧力が上昇しています。しかしサイクル計算上はあくまでコンプレッサの一種として取り扱うことができるため、パワータービンとファンとひとつの軸として、2軸タービンとして計算を行います。
2軸の場合出力マッチングが少しややこしくなります。回転数がそれぞれの軸で異なるため、場合によっては計算が収束しないことがあり、下手な初期値で計算すると泥沼にハマってしまいます。バイパス比が大きく、ほぼパワータービンとファンという場合は比較的収束しますが、コアセクションが2軸の場合は実機を事前予想するには入念な事前検討が必要です。
また、実際のガスタービン自体が1軸以上に多段化される傾向にあるため、作動範囲が狭くなりがちです。
多段マッチングやクローズドサイクルに興味がある方は今後も一緒にターボ機械シリーズで勉強してみましょう。
最後に
みなさんどうしたか？私は記事を書いてて途中で間違えたりしました(汗)。
りなこが最初にどれだけ燃料を入れるか、ってめちゃくちゃ適当なこと言ったけど、外部に取り出せる仕事ってやっぱり燃料から来るからあながち間違ってなかったのかも、と思えたかもしれません。本質的には火を焚べて、羽根車を回す装置ですから、単純に考えることも大事なのですね。
パズルみたいで楽しかった！前回ガスタービンの構造を見た時は難しそうで無理って思ったけれど簡素化して考えると意外と分かりやすかったかも。
今回は少し長くなりましたが、この理論は空気を使うほとんどのターボ機械で使用可能です。計算までしなくても、コンプレッサ/タービンマップ、P-Q曲線、パワーバランスや流体、エネルギーの流れと言った基本的な概念を少しでも理解してもらえたなら嬉しいです。
ガスタービンは非常にシンプルなコンセプトでありながら色々と奥が深く、工学系の人間ならきっと楽しめる機械です。
今回も最後まで読んで頂きありがとうございます。これからもターボ機械シリーズは少しずつ続けて行きたいと思っているのでお楽しみに。また次回お会いしましょう！
クレジット・参考文献
多軸多段についてもっと詳しく知りたい方：
NAL-TR-347：多軸ターボファンエンジンの設計点外性能
熱力学の教科書：熱力学JSMEテキストシリーズ
おすすめ教科書一覧：
[…] 【ターボ機械シリーズ②】ガスタービンシステム検討：ターボ機械のパワーマッチングについてガスタービンの出力を決定するタービンパワーマッチングについて解説します。ターボ機 […]
[…] 【ターボ機械シリーズ②】ガスタービンシステム検討：ターボ機械のパワーマッチングについてガスタービンの出力を決定するタービンパワーマッチングについて解説します。ターボ機 […]
詳しくご解説ありがとうございます！
理想的なブレイトンサイクルの理論熱効率について、P1/P2となっておりますが、P2/P1ではないでしょうか？すみません。気になったのでご連絡いたします。
読んで頂きありがとうございます！再確認しましたが、そのままで大丈夫です。理論効率ηは1-1/(膨張比^(γ-1/γ))のため、最初から割り算して表記しています。